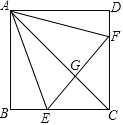
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤ ![]() ,其中正确结论有( )个
,其中正确结论有( )个
A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】C
【解析】∵四边形ABCD是正方形,△AEF是等边三角形,
∴AB=BC=CD=AD,AE=AF=EF,∠B=∠D=∠BCD=90°,∠EAF=60°,
∴△ABE≌△ADF,∠BAE+∠DAF=90°-60°=30°,
∴∠BAE=∠DAF=15°,BE=DF,(即①②正确);
∴BC-BE=DC-DF,即CE=CF,
又∵AE=AF,
∴点A、C都在线段EF的垂直平分线上,
∴AC垂直平分EF.(即③正确);
如下图,在AB上取点P连接PE,使PE=PA,则由∠BAE=15°可知∠BPE=30°,
设BE=DF=1,则PE=PA=2,在Rt△PEB中由勾股定理可得:PB=![]() ,
,
∴AB=BC=DC=![]() ,
,
∴CE=CF=BC-BE=![]() ,
,
∴EF=![]() EC=
EC=![]() ,
,
∵BE+DF=2,
∴BE+DF![]() EF.(即④错误);
EF.(即④错误);
∵S△CEF=![]() CE2=
CE2=![]() ,2S△ABE=
,2S△ABE=![]() AB·BE=
AB·BE=![]() ,
,
∴S△CEF=2S△ABE(即⑤正确);
综上所述,上述5个结论中,正确的有4个.
故选C.

-
科目: 来源: 题型:
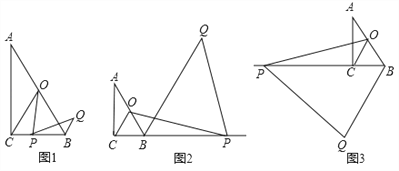
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.
(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)如图3,当点P在BC延长线上时,若∠BPO=15°,BP=4,请求出BQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣2x+4交y轴于点A,交抛物线
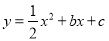 于点B(3,﹣2),抛物线经过点C(﹣1,0),交y轴于点D,点P是抛物线上的动点,作PE⊥DB交DB所在直线于点E.
于点B(3,﹣2),抛物线经过点C(﹣1,0),交y轴于点D,点P是抛物线上的动点,作PE⊥DB交DB所在直线于点E.(1)求抛物线的解析式;
(2)当△PDE为等腰直角三角形时,求出PE的长及P点坐标;
(3)在(2)的条件下,连接PB,将△PBE沿直线AB翻折,直接写出翻折点后E的对称点坐标.

-
科目: 来源: 题型:
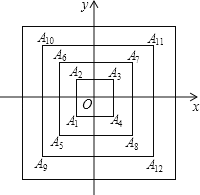
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2018的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节前夕,三位同学到某超市调研一种进价为80元的粽子礼盒的销售情况,请根据小梅提供的信息,解答小慧和小杰提出的问题.(价格取正整数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:
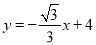 与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:(1)求出点A1的坐标,并判断点A1是否在直线l上;
(2)求出边A1C1所在直线的解析式;
(3)在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.

-
科目: 来源: 题型:
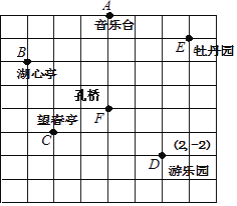
查看答案和解析>>【题目】王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴.y轴.只知道游乐园D的坐标为(2,﹣2),请你帮她画出坐标系,并写出其他各景点的坐标.
相关试题

