【题目】在精准扶贫中,某村的李师傅在县政府的扶持下,去年下半年,他对家里的3个温室大棚进行修整改造,然后,1个大棚种植香瓜,另外2个大棚种植甜瓜,今年上半年喜获丰收,现在他家的甜瓜和香瓜已全部售完,他高兴地说:“我的日子终于好了”.
最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜,他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:

现假设李师傅今年下半年香瓜种植的大棚数为x个,明年上半年8个大棚中所产的瓜全部售完后,获得的利润为y元.
根据以上提供的信息,请你解答下列问题:
(1)求出y与x之间的函数关系式;
(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚?才能使获得的利润不低于10万元.
参考答案:
【答案】(1)y=7500x+68000;(2)5.
【解析】
试题分析:(1)利用总利润=种植香瓜的利润+种植甜瓜的利润即可得出结论;
(2)利用(1)得出的结论大于等于100000建立不等式,即可确定出结论.
试题解析:(1)由题意得,y=(2000×12﹣8000)x+(4500×3﹣5000)(8﹣x)=7500x+68000;
(2)由题意得,7500x+6800≥100000,∴x≥![]() ,∵x为整数,∴李师傅种植的8个大棚中,香瓜至少种植5个大棚.
,∵x为整数,∴李师傅种植的8个大棚中,香瓜至少种植5个大棚.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+bx-c的图象与x轴两交点的坐标分别为(m,0),(-3m,0)(m≠0).
(1)证明4c=3b2
(2)若该函数图象的对称轴为直线x=1,试求二次函数的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=
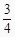 (x-1)2-3 .
(x-1)2-3 .
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】现在正是草莓热销的季节,某水果零售商店分两批次从批发市场共购进草莓40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.
(1)设第一、二次购进草莓的箱数分别为a箱、b箱,求a,b的值;
(2)若商店对这40箱草莓先按每箱60元销售了x箱,其余的按每箱35元全部售完.
①求商店销售完全部草莓所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.(注:按整箱出售,利润=销售总收入-进货总成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·天津)公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台,租车费用为400元,每辆乙种货车一次最多运送机器30台,租车费用为280元.
(1)设租用甲种货车x辆(x为非负整数),试填写表格:
表一:
租用甲种货车的数量 / 辆
3
7
x
租用的甲种货车最多运送机器的数量 / 台
135
租用的乙种货车最多运送机器的数量 / 台
150
表二:
租用甲种货车的数量 / 辆
3
7
x
租用甲种货车的费用/ 元
2800
租用乙种货车的费用 / 元
280
(2)若租用甲种货车x辆时,设两种货车的总费用为y元,试确定能完成此项运送任务的最节省费用的租车方案.
相关试题

