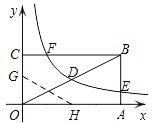
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(8,n)在边AB上,反比例函数![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=![]() .
.
(1)求反比例函数的解析式和n的值;
(2)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求G点的坐标.
参考答案:
【答案】(1)反比例函数的解析式为![]() ,n=1;
,n=1;
(2)G点的坐标为(0,2.5)
【解析】解:(1)在Rt△BOA中 ∵OA=8 ,∴AB=OA×tan∠BOA=4
∵点D为OB的中点,点B(8,4),∴点D(4,2)
又∵点D在的图象上 , ∴![]()
∴k=8 ∴![]()
又∵点E在图象上 ∴8n=8 ∴ n=1
(2)设点F(a,4),∴4a=8 ,∴CF=a=2
连结FG,设OG=t,则OG=FG=t CG=4-t
Rt△CGF中,GF2=CF2+CG2
∴t2=(4-t)2+12 ,∴t=2.5,∴=2.5
∴G点的坐标为(0,2.5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定一种新的运算“*”:对于任意实数x,y,满足x*y=x﹣y+xy.如3*2=3﹣2+3×2=7,则2*1=( )
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角形板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是( )

A.16
B.12
C.8
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
一列火车要以每秒20米的速度通过第一、第二两座铁桥(火车的长度忽略不计)过第二座铁桥比过第一座铁桥多50秒,已知铁桥的长度比第一座铁桥的长度的两倍短500米,求两座铁桥各自的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=36°,∠A=∠B,则∠A=_______°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形的内角和是外角和的3倍,求此多边形的边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
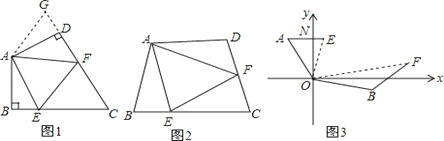
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=
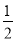 ∠BAD上述结论是否仍然成立,并说明理由;
∠BAD上述结论是否仍然成立,并说明理由;(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
相关试题

