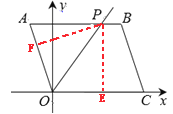
【题目】如图,□OABC的三个顶点分别为O(0,0),C(4,0),B(3,3),∠AOC的平分线OP交AB于点P,则点P的坐标为______________.

参考答案:
【答案】(![]() ,3).
,3).
【解析】
过点P作PE⊥x轴,PF⊥AO,垂足分别为点E、F,根据角平分线的性质得PE=PF,设OE=x,则OF=x,用含有x的代数式分别表示AF、PF和AP,然后利用勾股定理求解即可.
过点P作PE⊥x轴,PF⊥AO,垂足分别为点E、F,如图所示,
∵四边形ABCD是平行四边形,且B(3,3),C(4,0)
∴AB=OC=4,AO=BC=![]() ,
,
∴A(-1,0),
∴PE=3,
∵OP是∠AOC的平分线,
∴PE=PF=3,OE=OF,
设OE=x,则OF=x,AF=![]() -x,AP=x+1,
-x,AP=x+1,
在Rt△APF中,![]() ,
,
∴![]() ,解得x=
,解得x=![]() .
.
∴点P 的坐标为(![]() ,3).
,3).
故答案为:(![]() ,3).
,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A. x2-6=(10-x)2B. x2-62=(10-x)2
C. x2+62=(10-x)2D. x2+6=(10-x)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A,B,C三点,分别代表﹣36,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒.
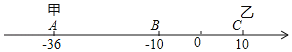
(1)问多少秒后,甲到A,B,C的距离和为60个单位?
(2)若乙的速度为6个单位/秒,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,问甲,乙在数轴上的哪个点相遇?
(3)在(1)(2)的条件下,当甲到A、B、C的距离和为60个单位时,甲调头返回.问甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
-
科目: 来源: 题型:
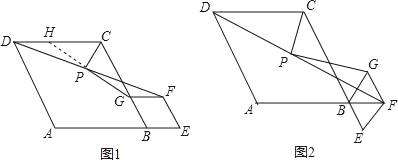
查看答案和解析>>【题目】阅读下列材料:问题:如图1,在菱形ABCD和菱形BEFG中,∠ABC=∠BEF=60°,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC,探究PG与PC的位置关系
小颖同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.
请你参考小颖同学的思路,探究并解决下列问题:
(1)请你写出上面问题中线段PG与PC的位置关系;
(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题申的其他条件不变(如图2).你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明,
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,任意两点A(
 ,
, 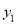 ),B(
),B(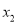 ,
, 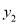 ),规定运算:①A⊕B=(
),规定运算:①A⊕B=(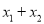 ,
, 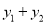 );②AB=
);②AB=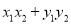 ;③当
;③当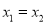 且
且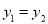 时,A=B,有下列四个命题:(1)若A(1,2),B(2,﹣1),则A⊕B=(3,1),AB=0;
时,A=B,有下列四个命题:(1)若A(1,2),B(2,﹣1),则A⊕B=(3,1),AB=0;(2)若A⊕B=B⊕C,则A=C;
(3)若AB=BC,则A=C;
(4)对任意点A、B、C,均有(A⊕B)⊕C=A⊕(B⊕C)成立,其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克)
-3
-2
-1.5
0
1
2.5
筐数
1
4
2
3
2
8
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价
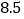 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:如图1,⊙
 与直线
与直线 都相切.不论⊙
都相切.不论⊙ 如何转动,直线
如何转动,直线 之间的距离始终保持不变(等于⊙
之间的距离始终保持不变(等于⊙ 的半径).我们把具有这一特性的图形称为“等宽曲线”.图2是利用圆的这一特性的例子.将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力就可以推动物体前进.据说,古埃及就是利用只有的方法将巨石推到金字塔顶的.
的半径).我们把具有这一特性的图形称为“等宽曲线”.图2是利用圆的这一特性的例子.将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力就可以推动物体前进.据说,古埃及就是利用只有的方法将巨石推到金字塔顶的.
拓展应用:如图3所示的弧三角形(也称为莱洛三角形)也是“等宽曲线”.如图4,夹在平行线
 之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变.若直线
之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变.若直线 之间的距离等于
之间的距离等于 ,则莱洛三角形的周长为
,则莱洛三角形的周长为  .
.
相关试题

