【题目】如图,CD是△ABC的中线,CE是△ABC的高,若AC=9,BC=12,AB=15.
(1)求CD的长.
(2)求DE的长.

参考答案:
【答案】(1)7.5;(2)2.1.
【解析】
(1)利用勾股定理的逆定理得到三角形ABC为直角三角形,再根据直角三角形的性质可求CD的长.
(2)根据三角形的面积公式可求CE,再根据勾股定理可求DE的长.
(1)由AC=9,AB=15,BC=12,
AC2+BC2=81+144=![]() = AB2
= AB2
∴∠ACB=90°,
∵点D是AB的中点,
∴CD=![]() AB=7.5;
AB=7.5;
(2)由∠ACB=90°,可得S△ABC=![]() AC·BC=
AC·BC=![]() AB·CE,
AB·CE,
∴![]() ×9×12=
×9×12=![]() ×15CE,
×15CE,
解得CE=7.2,
Rt△CDE中,DE=![]() =2.1.
=2.1.
故答案为:(1)7.5;(2)2.1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机老姚某天上午营运全是在东西走向的解放路上进行.如 果规定向东为正,向西为负,他这天上午行车里程(单位:km)如下:
+8,+6,﹣10,﹣3,+6,﹣5,﹣2,﹣7,+4,+8,﹣9,﹣12.
(1)将第几名乘客送到目的地时,老姚刚好回到上午出发点?
(2)将最后一名乘客送到目的地时,老姚距上午出发点多远?在出发点的东面 还是西面?
(3)若汽车耗油量为0.075L/km,这天上午老姚的出租车耗油多少L?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网站策划了A、B两种上网的月收费方式:
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
m
n
P
设每月上网学习时间为x(h)小时,方案A,B的收费金额分别为yA (元)、yB(元).
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)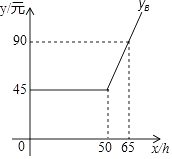
(1)m=;n=p= .
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费? -
科目: 来源: 题型:
查看答案和解析>>【题目】“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)
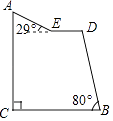
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD,CEFG按如图放置,点B,C,E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M,有下列结论:①EC=BP;②AP=AM;③∠BAP=∠GFP;④AB2+CE2=
 AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )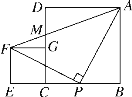
A. ①②③ B. ①③④ C. ①②④⑤ D. ①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,
(1)求证:∠A=90°.
(2)若DE=3,BD=4,求AE的长.

相关试题

