搜索
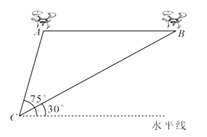
【题目】(2016广东省深圳市第20题)某兴趣小组借助无人飞机航拍校园，如图，无人飞机从A初飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°.B处的仰角为30°.已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度.(结果保留根号)
参考答案：
【答案】8+8
【解析】
试题分析：作AD⊥BC，BH⊥水平线，根据题意得出∠ABC=30°, ∠ACB=45°，根据三角函数的计算法则得出AD、CD和BD的长度，从而求出BC的长度，然后根据三角函数得出BH的长度，从而得出答案.
试题解析：如图，作AD⊥BC，BH⊥水平线 由题意∠ACH=75°，∠BCH=30°，AB∥CH
∴∠ABC=30°, ∠ACB=45° ∵AB=4×8=32m ∴AD=CD=AB·sin30°=16m BD=AB·cos30°=16m
∴BC=CD+BD=16+16m ∴BH=BC·sin30°=8+8m
-
科目： 来源： 题型：
查看答案和解析>>【题目】调查某种家用电器的使用寿命，合适的调查方法是______．
-
科目： 来源： 题型：
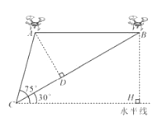
查看答案和解析>>【题目】(2016广西省贺州市第22题)如图，是某市一座人行天桥的示意图，天桥离地面的高BC是10米，坡面10米处有一建筑物HQ，为了方便使行人推车过天桥，市政府部门决定降低坡度，使新坡面DC的倾斜角∠BDC=30°，若新坡面下D处与建筑物之间需留下至少3米宽的人行道，问该建筑物是否需要拆除（计算最后结果保留一位小数）．（参考数据：
=1.414，
=1.732）
-
科目： 来源： 题型：
查看答案和解析>>【题目】若x2+mx+9是一个完全平方式，则m的值是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：
若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是【A，B】的好点．
如图1，点A表示的数为﹣1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是【A，B】的好点．
知识运用：
（1）如图1，表示0的点D到点A的距离是1，到点B的距离是2，那么点D 【A，B】的好点；（请在横线上填是或不是）
（2）如图2，M、N为数轴上两点，点M所表示的数为4，点N所表示的数为﹣2．数 所对应的点是【M，N】的好点（写出所有可能的情况）；
拓展提升：
（3）如图3，A、B为数轴上两点，点A所表示的数为﹣20，点B所表示的数为40．现有一只电子蚂蚁P从点B出发，以4个单位每秒的速度向左运动，到达点A停止．当经过几秒时，P、A和B中恰有一个点为其余两点的好点？（写出所有情况）
-
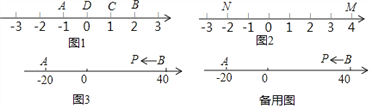
科目： 来源： 题型：
查看答案和解析>>【题目】若|m-n|=n-m,且|m|=4，|n|=3,则m+n的平方
-
科目： 来源： 题型：
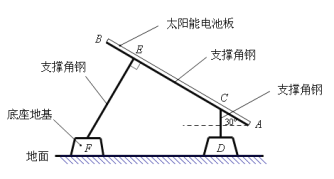
查看答案和解析>>【题目】(2016山西省第21题)太阳能光伏发电因其清洁、安全、便利、高效等特点，已成为世界各国普遍关注和重点发展的新兴产业，如图是太阳能电池板支撑架的截面图，其中的粗线表示支撑角钢，太阳能电池板与支撑角钢AB的长度相同，均为300cm，AB的倾斜角为
，BE=CA=50cm，支撑角钢CD，EF与底座地基台面接触点分别为D，F，CD垂直于地面，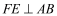
于点E．两个底座地基高度相同（即点D，F到地面的垂直距离相同），均为30cm，点A到地面的垂直距离为50cm，求支撑角钢CD和EF的长度各是多少cm（结果保留根号）
相关试题
