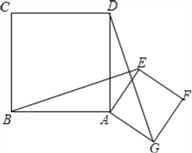
【题目】如图，已知正方形ABCD和正方形AEFG，连结BE、DG．

（1）请你判断线段BE和DG的关系并证明你的结论；

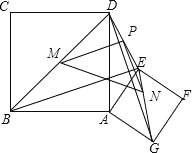
（2）连接BD、EG、DE，点M、N、P分别是BD、EG、DE的中点，连接MP，PN，MN，请你画出图形并判断△MPN的形状，说明理由

参考答案：

【答案】（1）BE和DG的关系是：BE=DG；BE⊥DG，证明见解析；（2）△MPN是等腰直角三角形，理由见解析

【解析】分析：（1）根据SAS证明△BEA与△DAG全等，再利用全等三角形的性质证明即可；（2）利用三角形中位线定理证得△MPN是等腰直角三角形；

本题解析：

（1）BE和DG的关系是：BE=DG；BE⊥DG

证明：∵正方形ABCD和正方形AEFG， ∴AB=AD，AE=AG，∠BAD=∠EAG=90°，∴∠BAD+∠DAE=∠EAG+∠DAE， ∴∠BAE=∠DAG，

∵在△BEA与△DAG中，

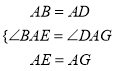
∴△BEA≌△DAG（SAS）；∴BE=DG，∠ADG=∠ABE，

∴∠BOD=∠BAD=90°，

∴BE⊥DG；

（2）证明：如图， 由三角形中位线定理可得：MP∥BE，MP= BE， PN∥DG，PN=DG，

∴PM=PN，∠MPN=∠BOD=90°，

即△MPN是等腰直角三角形；


关闭