【题目】如图,有两根直杆隔河相对,杆CD高30m,杆AB高20m,两杆相距50m.现两杆上各有一只鱼鹰,它们同时看到两杆之间的河面上E处浮起一条小鱼,于是以同样的速度同时飞下来夺鱼,结果两只鱼鹰同时到达,叼住小鱼.问两杆底部距鱼的距离各是多少?

参考答案:
【答案】两杆杆底到E处的水平距离分别是30m和20m.
【解析】根据题意结合勾股定理得出AB2+BE2=EC2+DC2,进而得出答案.
由题意可得AE=DE.在Rt△ABE和Rt△DEC中,
由勾股定理得AE2=AB2+BE2,DE2=EC2+CD2,
∴AB2+BE2=EC2+CD2,即202+BE2=(50-BE)2+302,
解得BE=30m,
则EC=50-30=20(m).
答:两杆杆底到E处的水平距离分别是30m和20m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知A(-1,5),B(4,2),C(-1,0)三点.
(1)点A的对称点A′的坐标为(1,-5),点B关于x轴的对称点B′的坐标为________,点C关于y轴的对称点C′的坐标为________;
(2)求(1)中的△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图.
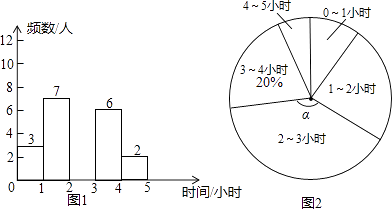
根据上述信息,解答下列问题:
(1)本次抽取的学生人数是;扇形统计图中的圆心角α等于;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,有一点P在线段AC上移动.若AB=AC=5,BC=6,则BP的最小值为________.
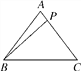
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组计划做一批“中国结”,如果每人做5个,那么比计划多了9个;如果每人做4个,那么比计划少15个.该小组共有多少人?计划做多少个“中国结”?
根据题意,小明、小红分别列出了尚不完整的方程如下:
小明:5x□( )=4x□( ); 小红:
 .
.(1)根据小明、小红所列的方程,其中“□”中是运算符号,“( )”中是数字,请你分别指出未知数x、y表示的意义.
小明所列的方程中x表示 ,
小红所列的方程中y表示 ;
(2)请选择小明、小红中任意一种方法,完整的解答该题目.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.

(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
相关试题

