【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E. 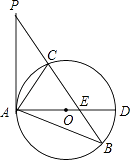
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点C,若ACAB=12,求AC的长.
参考答案:
【答案】
(1)证明:连接CD,如图,
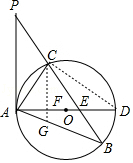
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD+∠D=90°,
∵∠PAC=∠PBA,
∠D=∠PBA,
∴∠CAD+∠PAC=90°,即∠PAD=90°,
∴PA⊥AD,
∴PA是⊙O的切线
(2)解:∵CF⊥AD,
∴∠ACF+∠CAF=90°,∠CAD+∠D=90°,
∴∠ACF=∠D,
∴∠ACF=∠B,
而∠CAG=∠BAC,
∴△ACG∽△ABC,
∴AC:AB=AG:AC,
∴AC2=AGAB=12,
∴AC=2 ![]()
【解析】(1)连接CD,如图,利用圆周角定理得到∠CAD+∠D=90°,再∠D=∠PBA,加上∠PAC=∠PBA,所以∠PAD=90°,然后根据切线的判定定理即可得到结论;(2)证明△ACG∽△ABC,再利用相似比得到AC2=AGAB=12,从而得到AC=2 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,点A、B在x轴上,AB⊥BC,AO=OB=2,BC=3
(1)写出点A、B、C的坐标.
(2)如图②,过点B作BD∥AC交y轴于点D,求∠CAB+∠BDO的大小.
(3)如图③,在图②中,作AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,第一次将三角形
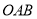 变换成三角形
变换成三角形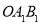 ,第二次将三角形
,第二次将三角形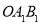 变换成三角形
变换成三角形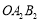 ,第三次将三角形变换成三角形
,第三次将三角形变换成三角形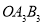 ,已知
,已知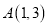 ,
,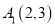 ,
, ,
, ,
,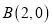 ,
,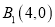 ,
,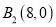 ,
, .
.(1)观察每次变换前后的三角形,找出规律,按这些变换规律将三角形
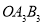 变换成三角形
变换成三角形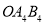 ,求
,求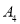 和
和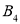 的坐标;
的坐标;(2)若按第(1)题的规律将三角形
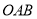 进行了
进行了 次变换,得到三角形
次变换,得到三角形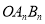 ,请推测
,请推测 和
和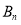 的坐标.
的坐标.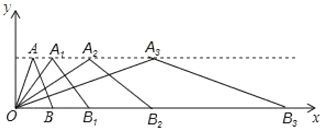
-
科目: 来源: 题型:
查看答案和解析>>【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时;
(2)小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=10x+10.请作出此函数图象,并利用图象回答:小王与小张在途中共相遇 次;
(3)请你计算第三次相遇的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,设
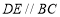 ,
,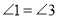 ,
,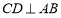 ,求证:
,求证: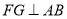 ;
;(2)若把(1)的题设中的“
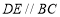 ”与结论中的“
”与结论中的“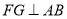 ”对调后,命题还成立吗?说明理由;
”对调后,命题还成立吗?说明理由;(3)若把(1)的题设中的“
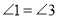 ”与结论中的“
”与结论中的“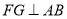 ”对调后,命题还成立吗?说明理由.
”对调后,命题还成立吗?说明理由.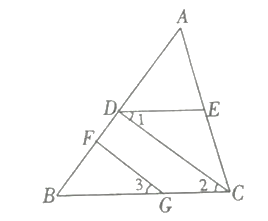
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=10,BC=16.点D在边BC上,且点D到边AB和边AC的距离相等.
(1)用直尺和圆规作出点D(不写作法,保留作图痕迹,在图上标注出点D);
(2)求点D到边AB的距离.

相关试题

