【题目】如图,抛物线y=ax2+bx+c经过点A(﹣3,0)、B(1,0)、C(0,3).
(1)求抛物线的解析式;
(2)若点P为抛物线在第二象限上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)抛物线y=﹣x2﹣2x+3;(2)点P的坐标为(﹣![]() ,
,![]() ,);(3)M(0,1).
,);(3)M(0,1).
【解析】
试题分析:(1)用待定系数法求出a,b,c,即可求解;
(2)用S=S△AOP+S△COP﹣S△AOC计算即可;
(3)设M(0,m)先判定△AOM≌△MFD,求出m即可.
试题解析:(1)∵抛物线y=ax2+bx+c经过点A(﹣3,0)、B(1,0)、C(0,3).
∴ ,∴
,∴ ,
,
∴抛物线y=﹣x2﹣2x+3;
(2)如图所示,

设P(x,﹣x2﹣2x+3),(﹣3<x<0),
∵OA=3,OC=3,
∴S=S△AOP+S△COP﹣S△AOC
=![]() OA×|yP|+
OA×|yP|+![]() OA×|xP|﹣
OA×|xP|﹣![]() OA×OC
OA×OC
=![]() ×3×(﹣x2﹣2x+3)+
×3×(﹣x2﹣2x+3)+![]() ×3×(﹣x)﹣
×3×(﹣x)﹣![]() ×3×3
×3×3
=﹣![]() x2﹣
x2﹣![]() x
x
=﹣![]() (x+
(x+![]() )2+
)2+![]() ,
,
∴当x=﹣![]() 时,S最大=
时,S最大=![]() ,
,
∴﹣(﹣![]() )2﹣2×(﹣
)2﹣2×(﹣![]() )+3=
)+3=![]() ,
,
∴点P的坐标为(﹣![]() ,
,![]() ),
),
(3)如图所示,当△ADM是等腰直角三角形,只能∠AMD=90°,
设M(0,m),过D作DF⊥x轴,∴F(0,4),∴OM=m,PM=4﹣m,DF=1,
∴△AOM≌△MFD,∴OM=DF=1,PM=OA=3,∴m=1,4-m=3,∴m=1,
∴M(0,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是某手机店1~4月份的统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( )
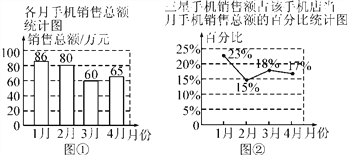
A. 4月份三星手机销售额为65万元
B. 4月份三星手机销售额比3月份有所上升
C. 4月份三星手机销售额比3月份有所下降
D. 3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明将父亲经营的便利店中“收入100元”记作“+100元”,那么“﹣80元”表示( )
A. 支出20元 B. 支出80元 C. 收入20元 D. 收入80元
-
科目: 来源: 题型:
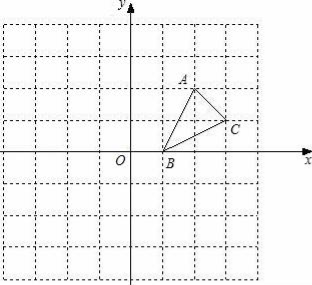
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球运动员在连续7场比赛中的得分(单位:分)依次为23,22,20,20,20,25,18.则这组数据的众数与中位数分别是( )
A.20分,22分B.20分,18分
C.20分,22分D.20分,20分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°,
求证:①AC=BD;②∠APB=50°.

-
科目: 来源: 题型:
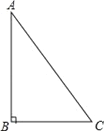
查看答案和解析>>【题目】已知Rt△ABC中,∠B=90°,
(1)根据要求作图(尺规作图,保留作图痕迹,不写画法):
①作∠BAC的平分线AD交BC于D;
②作线段AD的垂直平分线交AB于E,交AC于F,垂足为H;
③连接ED.
(2)在(1)的基础上写出一对全等三角形:△ ≌△ 并加以证明.
相关试题

