【题目】已知:如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°,
求证:①AC=BD;②∠APB=50°.

参考答案:
【答案】①证明见解析;②证明见解析.
【解析】①根据已知先证明∠AOC=∠BOD,再由SAS证明△AOC≌△BOD,所以AC=BD.②由△AOC≌△BOD,可得∠OAC=∠OBD,再结合图形,利用角的和差,可得∠APB=50°.
证明:①∵∠AOB=∠COD=50°,
∴∠AOB+∠BOC=∠COD+∠BOC,
∴∠AOC=∠BOD.
在△AOC和△BOD中,
AO=BO,∠AOC=∠BOD,OC=OD,
∴△AOC≌△BOD(SAS),
∴AC=BD;
②∵△AOC≌△BOD,
∴∠OAC=∠OBD,
∴∠OAC+∠AOB=∠OBD+∠APB,
∴∠OAC+60°=∠OBD+∠APB,
∴∠APB=50°.
“点睛”本题考查了全等三角形的性质和判定,三角形的内角和定理的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个等腰三角形的两边长为4、9,则它的周长为( )
A. 17B. 22C. 17或22D. 无法计算
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2+x=2,则下列说法中,正确的是( )
A.方程两根和是1
B.方程两根积是2
C.方程两根和是﹣1
D.方程两根积比两根和大2 -
科目: 来源: 题型:
查看答案和解析>>【题目】李老师布置了一道作图作业:“将一条12厘米的线段分成三段,然后用这一条线段为边作一个三角形.”下面是四个同学分线段的结果:小李:5厘米、5厘米、2厘米;小王:3厘米、4厘米、5厘米;小赵:3厘米、3厘米、6厘米;小张:4厘米、4厘米、4厘米.其中分法不正确的是( )
A.小李B.小王C.小赵D.小张
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:a(3a+4b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程ax2﹣bx﹣2019=0有一个根为x=﹣1,则a+b=_____.
-
科目: 来源: 题型:
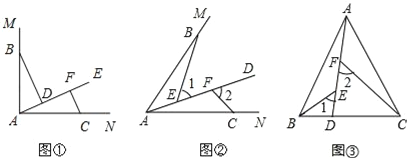
查看答案和解析>>【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
相关试题

