【题目】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度.已知动点A、B的速度比为1∶3(速度单位:1个单位长度/秒).

(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,满足OB=2OA?
参考答案:
【答案】(1)点A的运动速度为2个单位长度/秒,则点B的运动速度为6个单位长度/秒;
(2)点A表示的数是-4,点B表示的数是12;
(3)经过0.4秒或10秒,满足OB=2OA.
【解析】试题分析:(1)设动点A的速度是x单位长度/秒,那么动点B的速度是3x单位长度/秒,然后根据2秒后,两点相距16个单位长度即可列出方程解决问题;
(2)根据(1)的结果和已知条件即可得出.
(3)此问分两种情况讨论:设经过时间为x后,B在A的右边,若A在B的右边,列出等式解出x即可;
解:(1)设动点A的速度是x单位长度/秒,
根据题意得2(x+3x)=16
∴8x=16,
解得:x=2,
则3x=6.
答:动点A的速度是2单位长度/秒,动点B的速度是6单位长度/秒;
(2)标出A,B点如图,
![]() ;
;
(3)设x秒时,OB=2OA,
当B在A的右边,
根据题意得:12﹣6x=2(4+2x),
∴x=0.4,
当A在B的右边,
根据题意得:6x﹣12=2(4+2x),
∴x=10
∴0.4,10秒时OB=2OA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数的图象与反比例函数的图象交于A(﹣3,1)、B(m,3)两点,
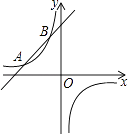
(1)求反比例函数和一次函数的解析式;
(2)写出使一次函数的值大于反比例函数的x的取值范围;
(3)连接AO、BO,求△ABO的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行了统计,绘制如图1和图2所示的统计图.根据图中信息解答下列问题:

(1)哪一种品牌粽子的销售量最大?
(2)补全图1中的条形统计图.
(3)写出A品牌粽子在图2中所对应的圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(2x+1)4=a0x4+a1x3+a2x2+a3x+a4,则a0+a2+a4的值为( )
A.82B.81C.42D.41
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种细胞的直径是5×10-4毫米,这个数是( )
A.0.05毫米B.0.005毫米C.0.0005毫米D.0.00005毫米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
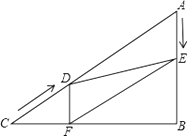
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,点P为BC上任意一点(可与点B或C重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最小值是( )
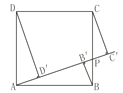
A. 1 B.
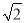 C.
C. 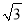 D.
D. 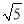
相关试题

