【题目】如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥DF交AB于点E,连接EG、EF. 
(1)求证:BG=CF;
(2)求证:EG=EF;
(3)请你判断BE+CF与EF的大小关系,并证明你的结论.
参考答案:
【答案】
(1)证明:∵BG∥AC,
∴∠C=∠GBD,
∵D是BC的中点,
∴BD=DC,
在△CFD和△BGD中

∴△CFD≌△BGD,
∴BG=CF.
(2)证明:∵△CFD≌△BGD,
∴DG=DF,
∵DE⊥GF,
∴EG=EF
(3)BE+CF>EF,
证明:∵△CFD≌△BGD,
∴CF=BG,
在△BGE中,BG+BE>EG,
∵由(2)知:EF=EG,
∴BG+CF>EF
【解析】(1)求出∠C=∠GBD,BD=DC,根据ASA证出△CFD≌△BGD即可.(2)根据全等得出GD=DF,根据线段垂直平分线性质得出即可.(3)根据全等得出BG=CF,根据三角形三边关系定理求出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.长度相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.直径是同一个圆中最长的弦
D.过三点能确定一个圆 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=
 ,y=
,y=  ,求代数式(x+y)2﹣(x﹣y)2的值.
,求代数式(x+y)2﹣(x﹣y)2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).

(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
-
科目: 来源: 题型:
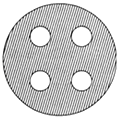
查看答案和解析>>【题目】如图,在一个大圆盘中,镶嵌着四个大小一样的小圆盘,已知大小圆盘的半径都是整数,阴影部分的面积为5πcm2 , 请你求出大小两个圆盘的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式-6ab2+18a2b2-12a3b2c的公因式是( )
A.-6ab2c B.-ab2 C.-6ab2 D.-6a3b2c
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=﹣3x2先向右平移4个单位,再向下平移5个单位,所得图象的解析式为( )
A. y=﹣3(x﹣4)2﹣5B. y=﹣3(x+4)2+5
C. y=﹣3(x﹣4)2+5D. y=﹣3(x﹣4)2﹣5
相关试题

