Question

【题目】如图，在平面直角坐标系中，点A、C的坐标分别为（0，8）、（6，0），以AC为直径作⊙O，交坐标轴于点B，点D是⊙O 上一点，且＝，过点D作DE⊥BC，垂足为E．

（1）求证：CD平分∠ACE；

（2）判断直线ED与⊙O的位置关系，并说明理由；

（3）求线段CE的长．

Answer 1

【答案】（1）参见解析；（2）相切，理由参见解析；（3）2．

【解析】试题分析：（1）利用圆内接四边形对角互补，可得出∠BAD＋∠BCD＝180°，利用邻补角性质可得出：∠BCD＋∠DCE＝180°，于是∠DCE＝∠BAD，又因为＝，等弧所对的圆周角相等，所以∠BAD＝∠ACD，等量代换：∠DCE＝∠ACD，于是得出CD平分∠ACE；（2）连接OD．证明OD⊥DE即可，因为上题已经得出∠DCE＝∠ACD，而又有OC=OD，∠ODC＝∠OCD，所以∠DCE＝∠ODC，所以OD∥BE，又因为DE⊥BC，所以OD⊥DE，进而得出结论；（3）延长DO交AB于点H，可得HO是△ABC的中位线，HO=3，因为∠ADC＝90°，O是AC的中点，所以OD＝AC＝5，HD＝3＋5＝8，而四边形BEDH是矩形（有三个角是直角的四边形是矩形），所以BE=HD=8，BC是6，从而求得CE值．

试题解析：（1）∵四边形ABCD是⊙O内接四边形，∴∠BAD＋∠BCD＝180°，又∵∠BCD＋∠DCE＝180°，∴∠DCE＝∠BAD，∵＝，∴∠BAD＝∠ACD，∴∠DCE＝∠ACD，∴CD平分∠ACE；（2）如图：连接OD．

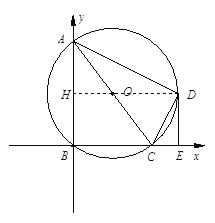
∵OC=OD，∴∠ODC=∠OCD，又∵∠DCE=∠ACD，∴∠DCE=∠ODC，∴OD∥BE，∴∠ODE+∠DEC=180° ， 又∵DE⊥BC，∴∠DEC=90°，∴∠ODE=90°∴OD⊥DE，又∵OD为半径，∴直线ED与⊙O相切；（3）如上图：延长DO交AB于点H，∵OD∥BE，O是AC的中点，∴H是AB的中点， ∴HO是△ABC的中位线， ∴HO=BC=3，因为AC为直径，∴∠ADC=90°，又∵O是AC的中点，∴OD=AC=×="5" ， ∴HD=3＋5=8，∵∠ABC=∠DEC=∠ODE=90°， ∴四边形BEDH是矩形，∴BE=HD=8，∴CE=8－6=2．