【题目】一家蔬菜公司收购某种绿色蔬菜140吨，准备加工后进行销售，销售后获利的情况如下表所示:

已知该公司的加工能力是：粗加工每天加工该种蔬菜的重量是精加工的3倍，但两种加工不能同时进行，受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售．

（1）若要求15天刚好加工完140吨蔬菜，如果绿色蔬菜先精加工20吨，剩下的再进行粗加工，正好按时完成，求精加工和粗加工每天各能加工的吨数．

（2）若要求将140吨蔬菜全部加工完不超过13天，并且两种加工方式都要有，先精加工后粗加工，问怎样分配加工时间（时间取整）利润最大？最大利润是多少？

参考答案：

【答案】（1）每天精加工4吨，则每天粗加工12吨；

（2）安排2天进行精加工，11天粗加工可获最大利润为148000元．

【解析】试题分析：（1）本题等量关系为：精加工天数+粗加工天数=15，进而列出方程求解即可．（2）首先求出精加工的天数的取值范围，然后表示W并求出W最大值．

试题解析: （1）设每天精加工x吨，则每天粗加工3 x吨，依题意得，

+= 15

解得：x=4，

经检验得：x=4是原方程的根；

则3x=12，

答：每天精加工4吨，则每天粗加工12吨；

（2）设精加工的时间为m天，依题意得

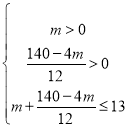
解得:

设加工这批蔬菜可获利W元，则

W=20004m+1000=140000+4000m（元）（0＜m≤2），

由一次函数性质知，W随m的增大而增大，　　　

故当m=2时，W取得最大值为140000+4000×2=148000（元），

答：安排2天进行精加工，11天粗加工可获最大利润为148000元．

关闭