【题目】为了提高学生学习数学的兴趣,端州区某中学举办了“数学实践活动周”活动.为了表彰在活动中表现突出的学生,学校购买了大、小笔记本分别65本和50本,共用了770元,其中每本大笔记本比小笔记本贵3元.
(1)求大、小笔记本的单价各为多少元?
(2)①学校仍需要购买上述的两种笔记本共160本(每种笔记本的单价不变).陈老师做完预算后,向财务处梁老师说:“我这次买这两种笔记本需支领1066元.”梁老师算了一下,说:“如果你用这些钱只买这两种笔记本,那么帐肯定算错了.”请你用学过的方程知识解释梁老师为什么说陈老师用这些钱只买这两种笔记本的帐算错了?
②陈老师突然想起,所做的预算还包括了包装这些奖品的包装纸.如果买包装纸的钱为小于10元而又多于5元的整数.请通过计算,直接写出买包装纸的钱用了元.
参考答案:
【答案】
(1)解:设小笔记本的单价为x![]() 元,则大笔记本的单价为
元,则大笔记本的单价为![]() 元.由题意得:
元.由题意得: ![]() ,
,
解得: ![]() ,则
,则 ![]()
答:小笔记本的单价为5元,大笔记本的单价为8元;
(2)["解:①设单价为5元的小笔记本为y![]() 本,所以单价为8元的大笔记本则为
本,所以单价为8元的大笔记本则为![]() 本.根据题意,得
本.根据题意,得 ![]() ,解得:
,解得: ![]() (不符合题意),所以陈老师肯定搞错了.② 8.设小笔记本买了
(不符合题意),所以陈老师肯定搞错了.② 8.设小笔记本买了 ![]() 本,买包装纸所需的钱是
本,买包装纸所需的钱是 ![]() 元,则可列方程:
元,则可列方程: ![]() ,整理得:
,整理得: ![]() ,因此,
,因此,![]() 必须是一个能给3整除的数.由“买包装纸的钱为小于10元而又多于5元的整数”可得:1)当
必须是一个能给3整除的数.由“买包装纸的钱为小于10元而又多于5元的整数”可得:1)当 ![]() 时,
时,![]() ,不符合题意.2)当
,不符合题意.2)当 ![]() 【解析】(1)设小笔记本的单价为x元,则大笔记本的单价为(x+3)元.根据“购买了大、小笔记本分别65本和50本,共用了770元”列方程求解;
【解析】(1)设小笔记本的单价为x元,则大笔记本的单价为(x+3)元.根据“购买了大、小笔记本分别65本和50本,共用了770元”列方程求解;
(2)①设单价为5元的小笔记本为y 本,所以单价为8元的大笔记本则为(160-y)本,根据“两种笔记本需支领1066元”列方程求解,得出y的值不是整数来说明;
②设小笔记本买了z本,买包装纸所需的钱是a元,列出方程5z+8(160-z)=1066-a,求出3z=214+a,再根据214+a必须是一个能给3整除的数依次讨论分析求出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=﹣x+3与直线l2:y=x+1相交于点A.并且l1交x轴于点B,l2交x轴于点C.若平面上有一点D,构成平行四边形ABDC,请写出D点坐标 .
-
科目: 来源: 题型:
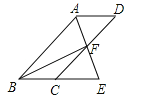
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
-
科目: 来源: 题型:
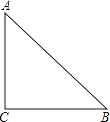
查看答案和解析>>【题目】如图所示,一块等腰直角三角形铁板,通过切割焊接成一个含有45°角的平行四边形,设计一种简要的方案并给出正确的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(m﹣1)x2+2x﹣1=0没有实数根,则m的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣2)2的对称轴是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
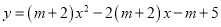 ,其中
,其中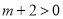 .
.(1)求该二次函数的对称轴方程;
(2)过动点C(0,
 )作直线
)作直线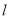 ⊥y轴.
⊥y轴.① 当直线
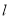 与抛物线只有一个公共点时, 求
与抛物线只有一个公共点时, 求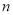 与
与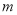 的函数关系;
的函数关系;② 若抛物线与x轴有两个交点,将抛物线在
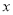 轴下方的部分沿
轴下方的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象. 当
轴翻折,图象的其余部分保持不变,得到一个新的图象. 当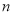 =7时,直线
=7时,直线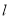 与新的图象恰好有三个公共点,求此时
与新的图象恰好有三个公共点,求此时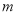 的值;
的值;(3)若对于每一个给定的x的值,它所对应的函数值都不小于1,求
 的取值范围.
的取值范围.
相关试题

