【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

请回答:BC+DE的值为________
参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数________
参考答案:
【答案】 ![]() 60°
60°
【解析】试题分析:请回答:由图2及其做法可得:EF=CD=3,CF=DE,所以BC+DE=BF,在Rt△BEF中由勾股定理可得BF=![]() ;解决问题:连接AE,CE,可证得四边形DCEF是平行四边形,四边形DCEF是平行四边形,进而可证△ACE是等边三角形,从而得∠AGF=∠ACE=60°.
;解决问题:连接AE,CE,可证得四边形DCEF是平行四边形,四边形DCEF是平行四边形,进而可证△ACE是等边三角形,从而得∠AGF=∠ACE=60°.
试题解析:解:BC+DE的值为![]() . 2分
. 2分
解决问题:
连接AE,CE,如图.

∵四边形ABCD是平行四边形,
∴AB //DC.
∵四边形ABEF是矩形,
∴AB //FE,BF=AE.
∴DC //FE.
∴四边形DCEF是平行四边形. 3分
∴CE //DF.
∵AC=BF=DF,
∴AC=AE=CE.
∴△ACE是等边三角形. 4分
∴∠ACE=60°.
∵CE∥DF,
∴∠AGF=∠ACE=60°. 5分
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣1,0,1,2,3这五个数中任取两数m,n,则二次函数y=﹣(x+m)2﹣n的顶点在x轴上的概率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A.2
B.8
C.2
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个边长为6的等边三角形电子跳蚤游戏盘.如果跳蚤开始时在AB边的P0处,且BP0=1,跳蚤第一步从P0跳到BC边的P1(第1次落点)处,且BP1=BP0;第二步从P1跳到AC边的P2(第2次落点)处,且CP2=CP1;第三步从P2 跳到AB边的P3(第3次落点)处,且AP3=AP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2017与P2018之间的距离为( )
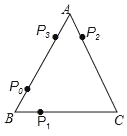
A. 1 B. 2 C. 3 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[
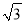 ]=1.现对72进行如下操作:72
]=1.现对72进行如下操作:72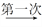 [
[ ]=8
]=8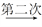 [
[ ]=2
]=2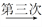 [
[ ]=1,这样对72进行3次操作后变为1,类似地,①对81进行________次操作后变为1;②进行3次操作后变为1的所有正整数中,最大的是________.
]=1,这样对72进行3次操作后变为1,类似地,①对81进行________次操作后变为1;②进行3次操作后变为1的所有正整数中,最大的是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,DC⊥BC,AE 平分∠BAD,DE 平分∠ADC,以下结论:①∠AED=90°;②点 E 是 BC 的中点;③DE=BE;④AD=AB+CD;其中正确的是( )
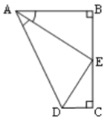
A. ①②③ B. ①②④ C. ①③④ D. ②③④
相关试题

