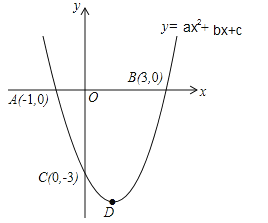
【题目】如图,抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1,
;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,4).
)或(1,4).
【解析】试题分析:(1)根据抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
(2)根据(1)中的解析式化为顶点式,即可得到此抛物线顶点D的坐标和对称轴;
(3)首先写出存在,然后运用分类讨论的数学思想分别求出各种情况下点P的坐标即可.
试题解析:(1)∵抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴ ,解得:
,解得:  ,即此抛物线的解析式是
,即此抛物线的解析式是![]() ;
;
(2)∵![]() =
=![]() ,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
(3)存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形,设点P的坐标为(1,y),分三种情况讨论:
①当PA=PD时![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1, ![]() );
);
②当DA=DP时, ![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1, ![]() )或(1,
)或(1, ![]() );
);
③当AD=AP时, ![]() =
=![]() ,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
由上可得,以点P、D、A为顶点的三角形是等腰三角形时,点P的坐标为(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,4).
)或(1,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校这两年在实验器材投资上的平均增长率为x,则可列方程: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形中的其中一个外角等于与它相邻的内角,那么这个三角形是( )
A.直角三角形B.锐角三角形C.钝角三角形D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2+2x+k﹣1=0的一个根是0,则k= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】最近几年,某市持续大面积雾霾天气让环保和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,某校在全校学生中抽取400名同学做了一次调查,调查结果共分为四个等组A.非常了解;B.比较了解;C.基本了解;D.不了解
根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾天气了解程度的
条形统计图
对雾霾天气了解程度的
扇形统计图
对雾霾天气了解程度的
统计表

图1

图2
对雾霾的了解程度
百分比
A.非常了解
5%
B.比较了解
m
C.基本了解
45%
D.不了解
n
请结合统计图表,回答下列问题:
(1)本次参与调查的学生选择“A.非常了解”的人数为__________人,m=__________,n=__________;
(2)请在图1中补全条形统计图;
(3)请计算在图2所示的扇形统计图中,D部分扇形所对应的圆心角是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,点C,D都在线段AB上,AC=2BC,点D是线段BC的中点,CD=2,求线段AB的长度;
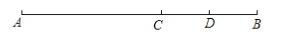
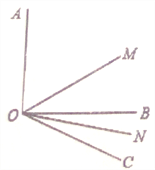
(2)如图所示.已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数a满足a2﹣2a=3,则3a2﹣6a﹣8的值为 .
相关试题

