【题目】阅读下面材料:
2019年4月底,“百年器象——清华大学科学博物馆筹备展”上展出了一件清华校友捐赠的历史文物“Husun型六分仪”(图①),它见证了中国人民解放军海军的发展历程.六分仪是测量天体高度的手提式光学仪器,它的主要原理是几何光学中的反射定律.观察测者手持六分仪(图②)按照一定的观测步骤(图③显示的是其中第6步)读出六分仪加油弧标尺上的刻度,再经过一定计算得出观察测点的地理坐标.

请大家证明在使用六分仪测量时用到的一个重要结论(两次反射原理).
已知:在图④所示的“六分仪原理图”中,所观测星体记为![]() ,两个反射镜面位于
,两个反射镜面位于![]() 两处,
两处,![]() 处的镜面的在直线
处的镜面的在直线![]() 自动与
自动与![]() 刻度线
刻度线![]() 保持平行(即
保持平行(即![]() ),并与
),并与![]() 处的镜面所在直线
处的镜面所在直线![]() 交于点
交于点![]() ,
,![]() 所在直线与水平线
所在直线与水平线![]() 交于点
交于点![]() ,六分仪上刻度线
,六分仪上刻度线![]() 与
与![]() 刻度线的夹角
刻度线的夹角![]() ,观测角为
,观测角为![]() .(请注意小贴士中的信息)
.(请注意小贴士中的信息)
求证:![]()

请在答题卡上完成对紫结论的以下填空及后续证明过程(后续证明无需标注理由).
证明:∵![]()
∴![]() ( )
( )
∵![]()
∴![]() ( )
( )
∵![]() ( )
( )
又∵![]() (小贴士已知),
(小贴士已知),
∴![]() .
.
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ( ).
( ).
即![]() .
.
补全证明过程:(请在答题卡上完成)
参考答案:
【答案】见解析;
【解析】
由![]() 得
得![]() ,再由三角形的外角的性质得
,再由三角形的外角的性质得![]() 与
与![]() ,进而可得结论.
,进而可得结论.
证明:如图
∵![]()
∴![]() ( 两直线平行,内错角相等 )
( 两直线平行,内错角相等 )
∵![]()
∴![]() ( 等量代换 )
( 等量代换 )
∵![]() ( 对顶角相等 )
( 对顶角相等 )
又∵![]() (小贴士已知),
(小贴士已知),
∴![]() .
.
∵![]() 是
是![]()
![]() 的外角,
的外角,
∴![]() ( 三角形的一个外角等于与它不相邻的两个内角之和 ).
( 三角形的一个外角等于与它不相邻的两个内角之和 ).
即![]() .
.
∵![]()
又∵![]()
∴![]()
∵![]() 是
是![]() 的外角
的外角
∴![]() .
.
即![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)2019年4月,中国新闻出版研究院发布了《第十六次全国国民阅读调查报告》,以下是小明根据该报告提供的数据制作的“2017-2018年我国未成年人图书阅读率统计图”的一部分.

报告中提到,2018年9-13周岁少年儿童图书阅读率比2017年提高了3.1个百分点,2017年我国0-17周岁未成年人图书阅读率为84.8%.
根据以上信息解决下列问题:
①写出图1中a的值;
②补全图1;
(2)读书社的小明在搜集资料的过程中,发现了《人民日报》曾经介绍过多种阅读法,他在班上同学们介绍了其中6种,并调查了全班40名同学对这6种阅读法的认可程度,制作了如下的统计表和统计图:

根据以上信息解决下列问题:
①补全统计表及图2;
②根据调查结果估计全年级500名同学最愿意使用“
 .精华提炼法”的人数.
.精华提炼法”的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】张老师从咸宁出发到外地参加教育信息化应用技术提高培训,他可以乘坐普通列车,也可以乘坐高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍.若高铁的平均速度(千米/小时)是普通列车平均速度的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间少3小时,求高铁的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两位同学,根据“关于x的一元二次方程kx2﹣(k+2)x+2=0”(k为实数)这一已知条件,他们各自提出了一个问题考查对方,问题如下:
甲:你能不解方程判断方程实数根的情况吗?
乙:若方程有两个不相等的正整数根,你知道整数k的值等于多少吗?请你帮助两人解决上述问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,点
,点 是平面上一点,射线
是平面上一点,射线 与直线
与直线 交于点
交于点 ,射线
,射线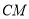 与直线
与直线 交于点
交于点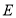 ,过点
,过点 作
作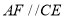 ,
, 与
与 所在的直线交于点
所在的直线交于点 .
.(1)如图1,当
 ,
, 时,写出
时,写出 的一个余角,并证明
的一个余角,并证明 ;
;(2)若
 ,
, .
.①如图2,当点
 在
在 内部时,用等式表示
内部时,用等式表示 与
与 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;②如图3,当点
 在
在 外部时,依题意补全图形,并直接写出用等式表示的
外部时,依题意补全图形,并直接写出用等式表示的 与
与 之间的数量关系.
之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,点D关于AB,AC的对称点分别是点E,F,四边形AEGF是平行四边形,则四边形AEGF面积的最小值是 ( )
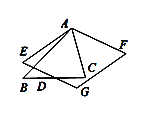
A. 1B.
 C.
C. 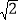 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形网格中建立平面斜坐标系
 ,对于其中的“格点
,对于其中的“格点 ”(落在网格线交点处的点),过点
”(落在网格线交点处的点),过点 分别做
分别做 轴,
轴,  轴的平行线,找到平行线与另一坐标轴的交点的
轴的平行线,找到平行线与另一坐标轴的交点的 坐标和
坐标和 坐标,记这个有序数对
坐标,记这个有序数对 为它的坐标,如
为它的坐标,如 ,
, ,规定当点在
,规定当点在 轴上时,
轴上时, 坐标为0,如
坐标为0,如 ;当点在
;当点在 轴上时,
轴上时, 坐标为0.
坐标为0.(1)原点
 的坐标为 ,格点
的坐标为 ,格点 的坐标为 .
的坐标为 .(2)在图中画出点
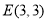 ,
,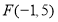 的位置;
的位置;(3)直线
 上的格点
上的格点 的坐标满足的条件是 (其中
的坐标满足的条件是 (其中 为整数).
为整数).
相关试题

