【题目】如图, ∠ADE+∠BCF=180°,BE平分∠ABC, ∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明: ∠E+∠F=90°.

(注:本题第(1)(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程)
解:(1) ADB∥C,理由如下:
∵∠ADE+∠BCF=180°(已知) ,
∠ADE+∠ADF=180°(平角的定义),
∴∠ADF__________ (______________________),
∴AD∥BC (__________________________);
(2)AB与EF的位置关系是:互相平行.
∵BE平分∠ABC(已知),
∴A∠BC=2∠ABE(角平分线定义).
又∵∠ABC=2∠E(已知),
∴2∠E=2∠ABE (____________________),
∴∠E=∠ABE(____________________),
∴______![]() _______ (________________________).
_______ (________________________).
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)欲证明AD∥BC,只要证明∠ADF=∠BCF即可;(2)结论:AB∥EF,只要证明∠E=∠ABE 即可;(3)①根据平行线的性质以及角平分线的定义即可证明;②只要证明∠OAB+∠OBA=90°即可解决问题;
(1)结论:AD∥BC.理由如下:
∵∠ADE+∠ADF=180,(平角的定义)
∠ADE+∠BCF=180,(已知)
∴∠ADF=∠BCF,(同角的余角相等)
∴AD∥BC
(2)结论:AB与EF的位置关系是:AB∥EF,
∵BE平分∠ABC,(已知)
∴∠ABE=12∠ABC.(角平分线的定义)
又∵∠ABC=2∠E,(已知),
即∠E=12∠ABC,
∴∠E=∠ABE.(等量代换)
∴AB∥EF.(内错角相等,两直线平行)
故答案为BCF,同角的余角相等,AB∥EF,ABE,等量代换,AB,EF,内错角相等,两直线平行。
(3)证明:①∵AB∥EF,
∴∠BAF=∠F,
∵∠BAD=2∠BAF,
∴∠BAD=2∠F.
②∵AD∥BC,
∴∠DAB+∠CBA=180,
∵∠OAB=12DAB,∠OBA=12∠CBA,
∴∠OAB+∠OBA=90,
∴∠EOF=∠AOB=90,
∴∠E+∠F=90.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.
(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.
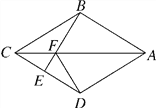
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.

(1)求线段BC的长;
(2)求线段MN的长;
(3)若C在线段AB延长线上,且满足AC﹣BC=b cm,M,N分别是线段AC,BC的中点,你能猜想MN的长度吗?请写出你的结论(不需要说明理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=
 ,b=2
,b=2 ,c=
,c= ;
;(2)a=5,b=7,c=9;
(3)a=2,b=
 ,c=
,c= ;
;(4)a=5,b=2
 ,c=1.
,c=1. -
科目: 来源: 题型:
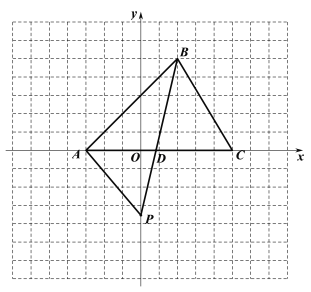
查看答案和解析>>【题目】(如图平面直角坐标系内,已知点A的坐标是(-3,0).
(1)点B的坐标为_______,点C的坐标为_____,∠BAC=______;
(2)求△ABC的面积;
(3)点P是y轴负半轴上的一个动点,连接BP交
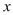 轴于点D,是否存在点P使得
轴于点D,是否存在点P使得△ADP与△BC的面积相等?若存在,请直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,CD⊥AB,垂足为D,如果CD=12,AD=16,BD=9,那么△ABC是直角三角形吗?请说明理由.

相关试题

