【题目】如图,点D,F在线段AB上,点E,G分别在线段BC和AC上,CD∥EF,∠1=∠2. 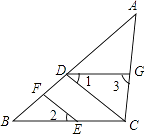
(1)判断DG与BC的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,试说明AB与CD有怎样的位置关系?
参考答案:
【答案】
(1)解:DG∥BC.
理由:∵CD∥EF,
∴∠2=∠BCD.
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC
(2)解:CD⊥AB.
理由:∵由(1)知DG∥BC,∠3=85°,
∴∠BCG=180°﹣85°=95°.
∵∠DCE:∠DCG=9:10,
∴∠DCE=95°× ![]() =45°.
=45°.
∵DG是∠ADC的平分线,
∴∠ADC=2∠CDG=90°,
∴CD⊥AB
【解析】(1)先根据CD∥EF得出∠2=∠BCD,再由∠1=∠2得出∠1=∠BCD,进而可得出结论;(2)根据DG∥BC,∠3=85°得出∠BCG的度数,再由∠DCE:∠DCG=9:10得出∠DCE的度数,由DG是∠ADC的平分线可得出∠ADC的度数,由此得出结论.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=﹣
 x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意实数k,关于x的方程x2-2(k+1)x+k2-1=0的根的情况为( )
A. 有两个相等的实数根B. 没有实数根
C. 有两个不相等的实数根D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2 , 直线l与l1、l2分别交于A、B两点,点M,N分别在l1、l2上,点M,N,P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
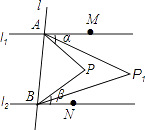
(1)当点P在l1与l2之间时. 求∠APB的大小(用含α、β的代数式表示);
(2)若∠APM的平分线与∠PBN的平分线交于点P1 , ∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 则∠AP1B= , ∠APnB= . (用含α、β的代数式表示,其中n为正整数)
(3)当点P不在l1与l2之间时. 若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知m2+m-1=0,则m3+2m2+2017= ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
⑴先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为_______,若A为随机事件,则m的取值为______;
⑵若从袋中随机摸出2个球,正好红球、黑球各1个,用列表法与树状图法求这个事件的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列一元二次方程;
(1)x2﹣4x﹣5=0
(2)(x﹣3)2=2(x﹣3)
相关试题

