【题目】如图,在平行四边形ABCD中,AB=2AD, AH⊥BC于点H,E是CD的中点,连接AE、 BE、HE.
(1)求证: AE⊥BE
(2)求证:∠DEH=3 ∠ EHC

参考答案:
【答案】证明见解析
【解析】(1)分别延长AE、BC交于点G,由角边角可证AED≌GEC,由全等三角形的性质可得AD=CG,AE=GE,即ABG是等腰三角形,由等腰三角形三线合一可得BE⊥AE;
(2)由直角三角形斜边上的中线等于斜边的一半可得HE=GE,由等边对等角得∠EHG=∠G,由平行四边形的性质得到AB=2AD由等边对等角证得∠CEG=∠G,即可得证.
(1)分别延长AE、BC交于点G,

∵四边形ABCD是平行四边形
∴AD=BC,AD//BC.
∴∠D=∠ECG
又∵E是CD的中点,
∴DE=CE,
又∵∠AED=∠GEC,
∴AED≌GEC,
∴AD=CG,AE=GE,
又∵AB=2AD,
∴AB=BC+CG=BG
∴BE是等腰三角形ABG底边上的中线
∴BE⊥AE.
(2)∵AH⊥BC,AE=GE..
∴HE是RtAHG斜边AG上的中线
∴HE=GE
∴∠EHG=∠G
∵四边形ABCD是平行四边形,AB=2AD
∴AB=CD=2AD
又∵E是CD的中点,AD=CG
∴AB=CD=2CE=2CG,即CE=CG
∴∠CEG=∠G
∴∠CEG=∠AED=∠G=∠EHG.
∵∠CEG=∠AED,∠AEH=∠G+∠EHG,∠DEH=∠AED+∠AEH
∴∠DEH=∠AED+∠G+∠EHG =3∠EHC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D,C关于抛物线的对称轴对称,直线AD与y轴相交于点E.

(1)求直线AD的解析式;
(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;
(3)如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线AM对称,连接M Q′,P Q′.当△PM Q′与□APQM重合部分的面积是APQM面积的 时,求APQM面积.
时,求APQM面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机的普及,微信
 一种聊天软件
一种聊天软件 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况 超额记为正,不足记为负
超额记为正,不足记为负 单位:斤
单位:斤 ;
;星期
一
二
三
四
五
六
日
与计划量的差值







(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校全体同学参加了二年级刘XX同学的捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
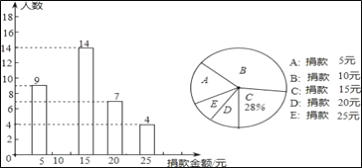
(1)本次共抽查学生 人,并将条形图补充完整;
(2)捐款金额的众数是 ,平均数是 ;
(3)在我校2200名学生中,捐款15元及以上(含15元)的学生估计有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2﹣3x+m=0的两实数根是( )
A.x1=1,x2=﹣1
B.x1=1,x2=2
C.x1=1,x2=0
D.x1=1,x2=3 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
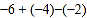 (2)
(2)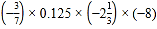
(3)(-2
 )-(+4.7)-(-0.4)+ (-3.3) (4)
)-(+4.7)-(-0.4)+ (-3.3) (4)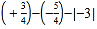
(5)
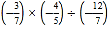 (6)(
(6)( -
- +
+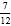 )×(-36)
)×(-36) (7)
 (8)—
(8)—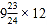 (用简便方法计算)
(用简便方法计算) -
科目: 来源: 题型:
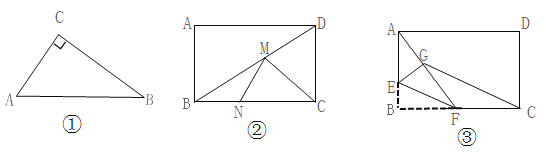
查看答案和解析>>【题目】(1)如图①,Rt△ABC中,∠C=90°,AC=3,BC=4.点D是AB边上任意一点,则CD的最小值为 。
(2)如图②,在矩形ABCD中,AB=3,BC=4.点M、N分别在BD、BC上。求CM+MN的最小值.
(3)如图③,在矩形ABCD中,AB=3,BC=4.点E是AB边上的一点,且AE=2,点F是BC边上的任意一点。把△BEF沿EF翻折,点B对应点G,连接AG、CG.四边形AGCD的面积的最小值是 。
相关试题

