【题目】已知△ABC中,∠A=30°.
(1)如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC=°. 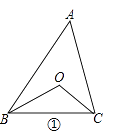
(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2 , 则∠BO2C=°. 
(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n﹣1个点),求∠BOn﹣1C(用n的代数式表示). 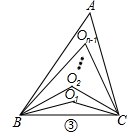
(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1 , 若∠BOn﹣1C=60°,求n的值.
参考答案:
【答案】
(1)105
(2)80
(3)解:∵点On﹣1是∠ABC与∠ACB的n等分线的交点,
∴∠On﹣1BC+∠On﹣1CB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() ×150°,
×150°,
∴∠BOn﹣1C=180°﹣ ![]() ×150°
×150°
(4)解:由(3)得:180°﹣ ![]() ×150°=60°,
×150°=60°,
解得:n=5.
【解析】解:∵∠BAC=30°, ∴∠ABC+∠ACB=150°,
⑴∵点O是∠ABC与∠ACB的角平分线的交点,
∴∠OBC+∠OCB= ![]() (∠ABC+∠ACB)=75°,
(∠ABC+∠ACB)=75°,
∴∠BOC=105°;
⑵∵点O2是∠ABC与∠ACB的三等分线的交点,
∴∠O2BC+∠O2CB= ![]() (∠ABC+∠ACB)=100°,
(∠ABC+∠ACB)=100°,
∴∠BO2C=80°;
【考点精析】掌握三角形的内角和外角和三角形的外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y,其中x=1,y=﹣1. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的平方和它的倒数相等,则这个数是( )
A.1
B.﹣1
C.±1
D.±1和0 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线y=kx﹣4经过点P(2,﹣8),求关于x的不等式kx﹣4≥0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校20名同学去工厂进行暑假实践活动,每名同学每天可以加工甲种零件5个或乙种零件4个,已知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元,若要使车间每天获利不低于1 800元,至少要派( )名同学加工乙种零件.
A. 11 B. 12 C. 13 D. 14
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A表示数a,点B表示数b,已知a、b满足(3a+b)2+|b﹣6|=0,
(1)求a、b的值;
(2)若在数轴上存在一点C,使得C到A的距离是C到B的距离的2倍,求点C表示的数;
(3)若小蚂蚁甲从点A处以1个单位长度/秒的速度向左运动,同时小蚂蚁乙从点B处以2个单位长度/秒的速度也向左运动,丙同学观察两只小蚂蚁运动,在它们刚开始运动时在原点O处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒.求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
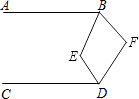
A.∠E=∠F
B.∠E+∠F=180°
C.3∠E+∠F=360°
D.2∠E﹣∠F=90°
相关试题

