【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有(填序号). 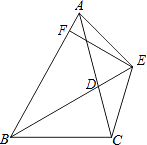
参考答案:
【答案】①②④
【解析】解:①∵BD为△ABC的角平分线,∴∠ABD=∠CBD,
在△ABD和△EBC中,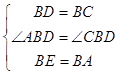 ,
,
∴△ABD≌△EBC(SAS),
∴①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,
∴②正确;
③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC,
∵BD为△ABC的角平分线,EF⊥AB,而EC不垂直与BC,
∴EF≠EC,
∴③错误;
④过E作EG⊥BC于G点,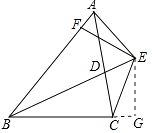
∵E是BD上的点,∴EF=EG,
在RT△BEG和RT△BEF中,![]() ,
,
∴RT△BEG≌RT△BEF(HL),
∴BG=BF,
在RT△CEG和RT△AFE中,![]() ,
,
∴RT△CEG≌RT△AFE(HL),
∴AF=CG,
∴BA+BC=BF+FA+BG﹣CG=BF+BG=2BF,
∴④正确.
所以答案是:①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2向左平移5个单位后得到的抛物线对应的函数解析式是( )
A.y=﹣x2+5
B.y=x2﹣5
C.y=(x﹣5)2
D.y=(x+5)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在
 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品经过连续两次降价,销售单价由原来200元降到168元.设平均每次降价的百分率为x,根据题意可列方程为( )
A.200(1﹣x)2=168B.200(1+x)2=168
C.168(1+x)2=200D.168(1﹣x)2=200
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°.

(1)用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(2)连结AP,若AC=4,BC=8时,试求BP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一种“二十四点”的游戏,其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其结果等于24.例如对1,2,3,4,可作如下运算:(1+2+3)×4=24(上述运算与4×(1+2+3)视为相同方法的运算)现有四个有理数3,4,
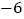 ,10,运用上述规则写出三种不同方法的运算式,可以使用括号,使其结果等于24.运算式分别为:
,10,运用上述规则写出三种不同方法的运算式,可以使用括号,使其结果等于24.运算式分别为:
(1);
(2);
(3)﹒ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于
 AD的长为半径在AD两侧作弧,交于两点M、N;
AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( )

A.2 B.4 C.6 D.8
相关试题

