【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.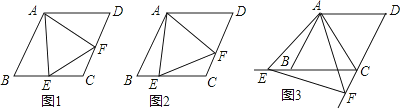
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
参考答案:
【答案】
(1)
解:结论AE=EF=AF.理由:如图1中 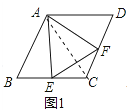
,连接AC,
∵四边形ABCD是菱形,∠B=60°,
∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ADC是等边三角形,
∴∠BAC=∠DAC=60°
∵BE=EC,
∴∠BAE=∠CAE=30°,AE⊥BC,
∵∠EAF=60°,
∴∠CAF=∠DAF=30°,
∴AF⊥CD,
∴AE=AF(菱形的高相等),
∴△AEF是等边三角形,
∴AE=EF=AF.
(2)
解:证明:如图2中 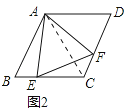
,∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAE,
在△BAE和△CAF中,
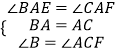 ,
,
∴△BAE≌△CAF,
∴BE=CF.
(3)
解: 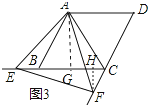
过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,
∵∠EAB=15°,∠ABC=60°,
∴∠AEB=45°,
在RT△AGB中,∵∠ABC=60°AB=4,
∴BG=2,AG=2 ![]() ,
,
在RT△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2 ![]() ,
,
∴EB=EG﹣BG=2 ![]() ﹣2,
﹣2,
∵△AEB≌△AFC,
∴AE=AF,EB=CF=2 ![]() ﹣2,∠AEB=∠AFC=45°,
﹣2,∠AEB=∠AFC=45°,
∵∠EAF=60°,AE=AF,
∴△AEF是等边三角形,
∴∠AEF=∠AFE=60°
∵∠AEB=45°,∠AEF=60°,
∴∠CEF=∠AEF﹣∠AEB=15°,
在RT△EFH中,∠CEF=15°,
∴∠EFH=75°,
∵∠AFE=60°,
∴∠AFH=∠EFH﹣∠AFE=15°,
∵∠AFC=45°,∠CFH=∠AFC﹣∠AFH=30°,
在RT△CHF中,∵∠CFH=30°,CF=2 ![]() ﹣2,
﹣2,
∴FH=CFcos30°=(2 ![]() ﹣2)
﹣2) ![]() =3﹣
=3﹣ ![]() .
.
∴点F到BC的距离为3﹣ ![]() .
.
【解析】(1)结论AE=EF=AF.只要证明AE=AF即可证明△AEF是等边三角形.
(2)欲证明BE=CF,只要证明△BAE≌△CAF即可.(3)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,根据FH=CFcos30°,因为CF=BE,只要求出BE即可解决问题. 本题考查四边形综合题、菱形的性质、等边三角形的判定、全等三角形的判定和性质等知识,解题的关键是灵活应用这些知识解决问题,学会添加常用辅助线,属于中考压轴题.
【考点精析】通过灵活运用菱形的性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.

(1)请判断:FG与CE的数量关系是 , 位置关系是;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题引入:

(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=(用α表示);如图②,∠CBO= ∠ABC,∠BCO=
∠ABC,∠BCO=  ∠ACB,∠A=α,则∠BOC=(用α表示)拓展研究:
∠ACB,∠A=α,则∠BOC=(用α表示)拓展研究:
(2)如图③,∠CBO= ∠DBC,∠BCO=
∠DBC,∠BCO=  ∠ECB,∠A=α,请猜想∠BOC=(用α表示),并说明理由.
∠ECB,∠A=α,请猜想∠BOC=(用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO= ∠DBC,∠BCO=
∠DBC,∠BCO=  ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=4
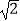 ,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F
,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F 
(1)求证: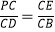 ;
;
(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由;
(3)设PE=x,△PBD的面积为S,求S与x之间的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3 时,求线段DH的长.
时,求线段DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)某校组织学生参加“周末郊游”.甲旅行社说:“只要一名学生买全票,则其余学生可享受半价优惠.”乙旅行社说:“全体学生都可按6折优惠”.已知全票价为240元.
(1)设学生人数为x,甲旅行社收费为y甲(元),乙旅行社收费为y乙(元),用含x的式子表示出y甲与y乙;
(2)就学生人数x讨论哪一家旅行社更优惠.
相关试题

