【题目】已知一次函数![]() 和
和![]() .
.
(1)在同一直角坐标系内,画出这两个函数的大致图象;

(2)直接写出:①函数![]() 与坐标轴围成的图形的面积为_______;
与坐标轴围成的图形的面积为_______;
②函数![]() 与坐标轴围成的图形的面积为________;
与坐标轴围成的图形的面积为________;
③这两个函数图象与![]() 轴围成的图形的面积为_________.
轴围成的图形的面积为_________.
(3)若反比例函数![]() 经过这两个函数图象的交点,则k的值为______.
经过这两个函数图象的交点,则k的值为______.
参考答案:
【答案】(1)画出这两个函数的大致图象见解析;(2)① ![]() ;②
;② ![]() ;③
;③ ![]() ;(3)3.
;(3)3.
【解析】
(1)把x=0,x=-1分别代入![]() 得出y值,描出两点,作出过两点的直线即可得
得出y值,描出两点,作出过两点的直线即可得![]() 的图象;把x=-1,x=-2分别代入
的图象;把x=-1,x=-2分别代入![]() 得出y值,描出两点,作出过两点的直线即可得
得出y值,描出两点,作出过两点的直线即可得![]() 的图象;
的图象;
(2)①分别令x=0,y=0,可分别求出x、y的值,根据直线与坐标轴围成的图形的面积=![]() |x||y|即可得答案;
|x||y|即可得答案;
②分别令x=0,y=0,可分别求出x、y的值,根据直线与坐标轴围成的图形的面积=![]() |x||y|即可得答案;
|x||y|即可得答案;
③由①②可知两直线与x轴的交点坐标,联立两直线解析式,解方程组可求出两直线的交点坐标,即可求出两个函数图象与![]() 轴围成的图形的面积;
轴围成的图形的面积;
(3)把两图象的交点坐标代入反比例函数解析式可求出k值,即可得答案.
(1)当x=0时,![]() =1,当x=-1时,
=1,当x=-1时,![]() =-3,
=-3,
当x=-1时,![]() =-3,当x=-2时,
=-3,当x=-2时,![]() =-1,
=-1,
∴两个函数的大致图象如图所示:
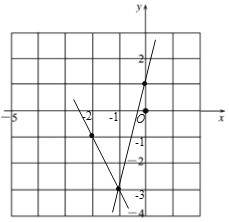
(2)①当x=0时,y=4x+1=1,
当y=0时,4x+1=0,
解得:x=![]() ,
,
∴函数![]() 与坐标轴围成的图形的面积为
与坐标轴围成的图形的面积为![]() ×|
×|![]() |×|1|=
|×|1|=![]() ,
,
故答案为:![]()
②当x=0时,y=-2x-5=-5,
当y=0时,-2x-5=0,
解得:x=![]() ,
,
∴函数y=-2x-5与坐标轴围成的图形的面积为![]() ×|
×|![]() |×|-5|=
|×|-5|=![]() ,
,
故答案为:![]()
③联立两直线解析式得:![]() ,
,
解得:![]() ,
,
∴两直线的交点坐标为(-1,-3),
由①②可知两直线与x轴当交点坐标为(![]() ,0)和(
,0)和(![]() ,0),
,0),
∴两个函数图象与![]() 轴围成的图形的面积为
轴围成的图形的面积为![]() ×|
×|![]() -(
-(![]() )|×|-3|=
)|×|-3|=![]() ,
,
故答案为:![]()
(3)∵两直线的交点坐标为(-1,-3),
∴k=(-1)×(-3)=3,
故答案为:3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量
 (毫克)随时间
(毫克)随时间 (小时)的变化情况如图所示,当成年人按规定剂量服药后.
(小时)的变化情况如图所示,当成年人按规定剂量服药后.
(1)当
 时,
时, 与
与 之间的函数关系式是________;
之间的函数关系式是________;(2)当
 时,
时, 与
与 之间的函数关系式是______;
之间的函数关系式是______;(3)如果每毫升血液中含药量
 毫克或
毫克或 毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时.
毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是坐标原点,直线OA与双曲线
 在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=
在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB= .
. (1)求双曲线的解析式;
(2)直线AC与y轴交于点C(0,1),与x轴交于点D,求D点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有三张正面分别标有数字:-1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线
 上的概率.
上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

-
科目: 来源: 题型:
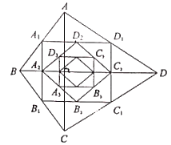
查看答案和解析>>【题目】如图,四边形
 中,
中, 顺次连接四边形
顺次连接四边形 各边中点,得到四边形
各边中点,得到四边形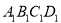 ,再顺次连接四边形
,再顺次连接四边形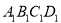 各边中点,得到四边形
各边中点,得到四边形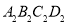 ...如此进行下去,得到四边形
...如此进行下去,得到四边形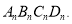 则下列结论正确的个数有( )
则下列结论正确的个数有( )①四边形
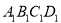 是矩形;②四边形
是矩形;②四边形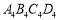 是菱形;③四边形
是菱形;③四边形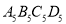 的周长为
的周长为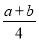 ; ④四边形
; ④四边形 的面积是
的面积是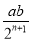 .
.
A.
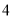 个B.
个B.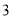 个C.
个C.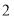 个D.
个D.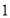 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形
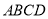 的边
的边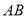 为边作等边三角形
为边作等边三角形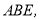 连接
连接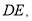 则
则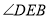 的度数为______.
的度数为______.
相关试题

