【题目】如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).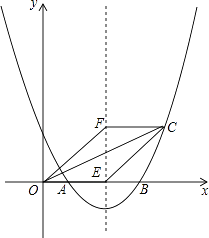
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:把点A(1,0)和B(4,0)代入y=ax2+bx+2得,
![]() ,
,
解得 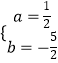 ,
,
所以,抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)
解:方法一:
抛物线的对称轴为直线x= ![]() ,
,
∵四边形OECF是平行四边形,
∴点C的横坐标是 ![]() ×2=5,
×2=5,
∵点C在抛物线上,
∴y= ![]() ×52﹣
×52﹣ ![]() ×5+2=2,
×5+2=2,
∴点C的坐标为(5,2)
方法二:
∵FC∥x轴,∴当FC=OE时,四边形OECF是平行四边形.
设C(t, ![]() ),
),
∴F( ![]() ,
, ![]() +2),
+2),
∴t﹣ ![]() =
= ![]() ,
,
∴t=5,C(5,2)
(3)
解:方法一:
设OC与EF的交点为D,
∵点C的坐标为(5,2),
∴点D的坐标为( ![]() ,1),
,1),
①点O是直角顶点时,易得△OED∽△PEO,
∴ ![]() ,
,
即 ![]() =
= ![]() ,
,
解得PE= ![]() ,
,
所以,点P的坐标为( ![]() ,﹣
,﹣ ![]() );
);
②点C是直角顶点时,同理求出PF= ![]() ,
,
所以,PE= ![]() +2=
+2= ![]() ,
,
所以,点P的坐标为( ![]() ,
, ![]() );
);
③点P是直角顶点时,由勾股定理得,OC= ![]() =
= ![]() ,
,
∵PD是OC边上的中线,
∴PD= ![]() OC=
OC= ![]() ,
,
若点P在OC上方,则PE=PD+DE= ![]() +1,
+1,
此时,点P的坐标为( ![]() ,
, ![]() ),
),
若点P在OC的下方,则PE=PD﹣DE= ![]() ﹣1,
﹣1,
此时,点P的坐标为( ![]() ,
, ![]() ),
),
综上所述,抛物线的对称轴上存在点P( ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),使△OCP是直角三角形
),使△OCP是直角三角形
方法二:
∵点P在抛物线的对称轴上,设P( ![]() ,t),O(0,0),C(5,2),
,t),O(0,0),C(5,2),
∵△OCP是直角三角形,∴OC⊥OP,OC⊥PC,OP⊥PC,
①OC⊥OP,∴KOC×KOP=﹣1,∴ ![]() ,
,
∴t=﹣ ![]() ,∴P(
,∴P( ![]() ,﹣
,﹣ ![]() ),
),
②OC⊥PC,∴KOC×KPC=﹣1,∴ ![]() =﹣1,
=﹣1,
∴t= ![]() ,P(
,P( ![]() ,
, ![]() ),
),
③OP⊥PC,∴KOP×KPC=﹣1,∴ ![]() ,
,
∴4t2﹣8t﹣25=0,∴t= ![]() 或
或 ![]() ,
,
点P的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),
),
综上所述,抛物线的对称轴上存在点P( ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),使△OCP是直角三角形.
),使△OCP是直角三角形.
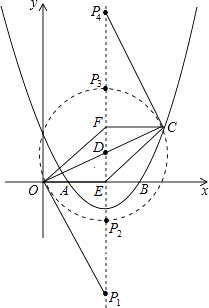
【解析】方法一:(1)把点A、B的坐标代入函数解析式,解方程组求出a、b的值,即可得解;(2)根据抛物线解析式求出对称轴,再根据平行四边形的对角线互相平分求出点C的横坐标,然后代入函数解析式计算求出纵坐标,即可得解;(3)设AC、EF的交点为D,根据点C的坐标写出点D的坐标,然后分①点O是直角顶点时,求出△OED和△PEO相似,根据相似三角形对应边成比例求出PE,然后写出点P的坐标即可;②点C是直角顶点时,同理求出PF,再求出PE,然后写出点P的坐标即可;③点P是直角顶点时,利用勾股定理列式求出OC,然后根据直角三角形斜边上的中线等于斜边的一半可得PD= ![]() OC,再分点P在OC的上方与下方两种情况写出点P的坐标即可.
OC,再分点P在OC的上方与下方两种情况写出点P的坐标即可.
方法二:(1)略.(2)因为四边形OECF是平行四边形,且FC∥x轴,列出F,C的参数坐标,利用FC=OE,可求出C点坐标.(3)列出点P的参数坐标,分别列出O,C两点坐标,由于△OCP是直角三角形,所以分别讨论三种垂直的位置关系,利用斜率垂直公式,可求出三种情况下点P的坐标.
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y1=﹣
 x﹣1与反比例函数y2=
x﹣1与反比例函数y2= 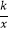 的图象交于点A(﹣4,m).
的图象交于点A(﹣4,m). 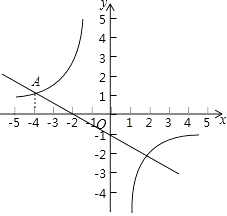
(1)观察图象,在y轴的左侧,当y1>y2时,请直接写出x的取值范围;
(2)求出反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,BF切⊙O于点B,AF交⊙O于点D,点C在DF上,BC交⊙O于点E,且∠BAF=2∠CBF,CG⊥BF于点G,连接AE.
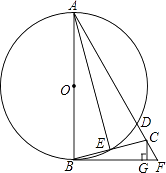
(1)直接写出AE与BC的位置关系;
(2)求证:△BCG∽△ACE;
(3)若∠F=60°,GF=1,求⊙O的半径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售.按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:

(1)设装运A种脐橙的车辆数为
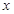 ,装运B种脐橙的车辆数为
,装运B种脐橙的车辆数为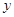 ,求
,求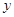 与
与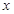 之间的函数关系式;
之间的函数关系式;(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,把两数相乘,积为1的是( )
A.2和-2
B.-2和
C. 和
和 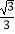
D. 和-
和- 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题12分)如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别O(0,0),A(3,
 ),B(9,5
),B(9,5  ),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,
),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,  ,
,  (单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.

(1)求AB所在直线的函数表达式.
(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值.
(3)在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在矩形ABCD中,AB=10 cm,BC=8 cm.点P从点A出发,沿A→B→C→D的路线运动,到点D停止;点Q从点D出发,沿D→C→B→A的路线运动,到点A停止.若点P、点Q同时出发,点P的速度为每秒1 cm,点Q的速度为每秒2 cm,a秒时,点P、点Q同时改变速度,点P的速度变为每秒b cm,点Q的速度变为每秒d cm.图②是点P出发x秒后△APD的面积S1(cm2)与时间x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与时间x(秒)的函数关系图象.
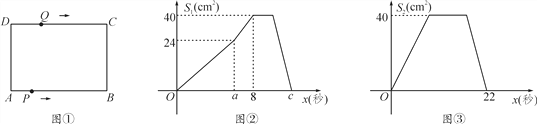
(1)参照图②,求a、 b及图②中c的值;
(2)求d的值;
(3)设点P离开点A的路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后,y1、y2与出发后的运动时间x(秒)的函数关系式,并求出点P、点Q相遇时x的值;
(4)当点Q出发__ __秒时,点Q的运动路程为25 cm.
相关试题

