【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角形的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
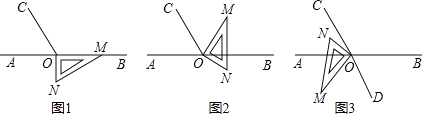
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 (直接写出结果);
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,OD为∠BOM平分线.请探究:∠MOD与∠NOC之间的数量关系,并说明理由.
参考答案:
【答案】(1)见解析;(2)12秒或48秒;(3)2∠MOD+∠NOC=150°,理由见解析.
【解析】
(1)如图2中,设ON的反向延长线为OD,根据余角的性质和对顶角的性质可证明∠COD=∠AOD;
(2)分两种情形分别构建方程即可解决问题;
(3)结论:∠AOM=∠NOC+30°.根据角的和差定义判断即可.
(1)解:直线ON平分∠AOC,设ON的反向延长线为OD,
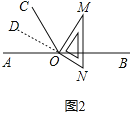
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON,
∴∠COD=∠AOD,
即直线ON平分∠AOC.
(2)解:由题意5t=60°或5t=240°,
解得t=12或48,
故答案为12秒或48秒.
(3)解:结论:∠AOM=∠NOC+30°.
理由:∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON,∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°,
即∠AOM=∠NOC+30°.
∵OD为∠BOM平分线,
∴∠BOM=2∠MOD,
∵∠AOM+∠BOM=180°,
∴∠AOM=180°-2∠MOD,
∴180°-2∠MOD=∠NOC+30°,
∴2∠MOD+∠NOC=150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现在平均每天比原计划多生产 50 台机器,现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同.
(1)现在平均每天生产多少台机器;
(2)生产 3000 台机器,现在比原计划提前几天完成.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个有50个奇数排成的数阵,用如图所示的框去框住四个数,并求出这四个数的和,在下列给出的备选答案中,有可能是这四个数的和的是( )
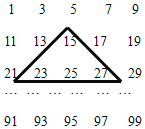
A. 114 B. 122 C. 220 D. 84
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(
 ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).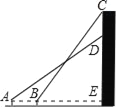
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 与函数
与函数 的图象交于
的图象交于 ,
,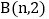 两点,
两点,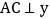 轴于C,
轴于C,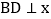 轴于D
轴于D 求k的值;
求k的值; 根据图象直接写出
根据图象直接写出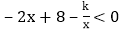 的x的取值范围;
的x的取值范围; 是线段AB上的一点,连接PC,PD,若
是线段AB上的一点,连接PC,PD,若 和
和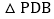 面积相等,求点P坐标.
面积相等,求点P坐标.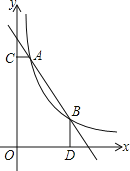
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
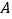 在数轴上对应的数为
在数轴上对应的数为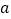 ,点
,点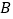 对应的数为
对应的数为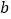 ,且
,且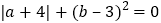 .
.
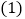 则
则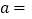 ________,
________,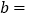 ________;并将这两个数在数轴上所对应的点
________;并将这两个数在数轴上所对应的点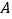 ,
,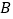 表示出来;
表示出来;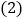 数轴上在
数轴上在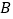 点右边有一点
点右边有一点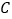 到
到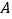 、
、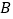 两点的距离和为
两点的距离和为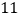 ,若点
,若点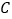 的数轴上所对应的数为
的数轴上所对应的数为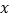 ,求
,求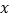 的值;
的值;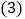 若点
若点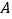 ,点
,点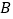 同时沿数轴向正方向运动,点
同时沿数轴向正方向运动,点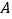 运动的速度为
运动的速度为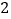 单位/秒,点
单位/秒,点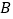 运动的速度为
运动的速度为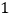 单位/秒,若
单位/秒,若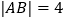 ,求运动时间
,求运动时间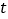 的值.
的值.(温馨提示:
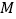 、
、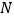 之间距离记作
之间距离记作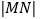 ,点
,点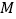 、
、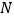 在数轴上对应的数分别为
在数轴上对应的数分别为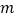 、
、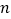 ,则
,则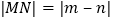 .)
.)
相关试题

