搜索
【题目】下表是某校女子羽毛球队队员的年龄分布：
年龄/岁 | 13 | 14 | 15 | 16 |
人数 | 1 | 1 | 2 | 1 |
则该校女子排球队队员年龄的中位数为__________岁.
参考答案：
【答案】15.
【解析】
中位数有2种情况，共有2n+1个数据时，从小到大排列后,，中位数应为第n+1个数据,可见,大于中位数与小于中位数的数据都为n个；共有2n+2个数据时,从小到大排列后,中位数为中间两个数据平均值,大小介于这两个数据之间，可见大于中位数与小于中位数的数据都为n+1个，所以这组数据中大于或小于这个中位数的数据各占一半，中位数有一个.
解：总数据有5个，中位数是从小到大排，第3个数据为中位数,即15为这组数据的中位数.
故答案为：15
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据下列条件可列出一元一次方程的是( )
A. a与1的和的3倍
B. 甲数的2倍与乙数的3倍的和
C. a与b的差的20%
D. 一个数的3倍是5
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的袋中装有红、白、黄3种颜色的若干个小球，它们除颜色外完全相同．每次从袋中摸出1个球，记下颜色后放回搅匀再摸．摸球实验中，统计得到下表中的数据：
摸球次数
10
20
50
100
150
200
250
300
400
500
出现红球的频数
4
9
16
31
44
61
74
92
118
147
出现白球的频数
1
4
16
36
52
61
75
85
123
151
由此可以估计摸到黄球的概率约为________（精确到0.1）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某种药品说明书上标明保存温度是（20±3）0C，则该药品在（ ）范围内保存最合适.
A. 170C~200C B. 200C ~230C C. 170C ~230C D. 170C ~240C
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列4个事件：①异号两数相加，和为负数；②异号两数相减，差为正数；③异号两数相乘，积为正数；④异号两数相除，商为负数．必然事件是________，不可能事件是________，随机事件是________．（将事件的序号填上即可）
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列关于单项式乘法的说法中不正确的是（ ）
A. 单项式之积不可能是多项式；
B. 单项式必须是同类项才能相乘；
C. 几个单项式相乘，有一个因式为0，积一定为0；
D. 几个单项式的积仍是单项式
-
科目： 来源： 题型：
查看答案和解析>>【题目】著名的瑞士数学家欧拉曾指出：可以表示为四个整数平方之和的甲、乙两数相乘，其乘积仍然可以表示为四个整数平方之和，即
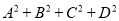，这就是著名的欧拉恒等式，有人称这样的数为“不变心的数”．实际上，上述结论可减弱为：可以表示为两个整数平方之和的甲、乙两数相乘，其乘积仍然可以表示为两个整数平方之和．【动手一试】
试将
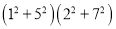改成两个整数平方之和的形式． 
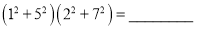；【阅读思考】
在数学思想中，有种解题技巧称之为“无中生有”．例如问题：将代数式
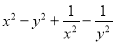改成两个平方之差的形式．解：原式
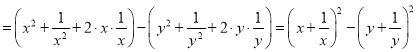﹒【解决问题】
请你灵活运用利用上述思想来解决“不变心的数”问题：将代数式
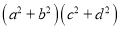改成两个整数平方之和的形式（其中a、b、c、d均为整数），并给出详细的推导过程﹒
相关试题
