【题目】在矩形ABCD中,AB=10,BC=12,E为DC的中点,连接BE,作AF⊥BE,垂足为F.

(1)求证:△BEC∽△ABF;
(2)求AF的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:由矩形ABCD中,AB=10,BC=12,E为DC的中点,由勾股定理可求得BE的长,又由AF⊥BE,易证得△ABF∽△BEC,然后由相似三角形的对应边成比例,求得AF的长.
试题解析:(1)证明:在矩形ABCD中,有
∠C=∠ABC=∠ABF+∠EBC=90°,
∵AF⊥BE,∴∠AFB=∠C=90°
∴∠ABF+∠BAF=90°
∴∠BAF=∠EBC
∴△BEC∽△ABF
(2)解:在矩形ABCD中,AB=10,∴CD=AB=10,
∵E为DC的中点,∴CE=5,
又BC=12,在Rt△BEC中,由勾股定理得BE=13,
由△ABF∽△BEC得
![]()
即![]() ,解得AF=
,解得AF=![]()
考点: 1.相似三角形的判定与性质;2.勾股定理;3.矩形的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长为( )

A.1
B.4﹣2
C.
D.3 ﹣4
﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某油箱容量为60 L的汽车,加满汽油后行驶了100 Km时,油箱中的汽油大约消耗了
 ,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )A. y=0.12x,x>0 B. y=60﹣0.12x,x>0 C. y=0.12x,0≤x≤500 D. y=60﹣0.12x,0≤x≤500
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学玩抽纸牌比大小的游戏,规则是:“甲将同一副牌中正面分别标有数字1,3,6的三张牌洗匀后,背面朝上放置在桌面上,随机抽一次且一次只抽一张,记下数字;乙将同一副牌中正面分别标有数字2,3,4的三张牌洗匀后,背面朝上放置在桌面上,随机抽一次且一次只抽一张,记下数字;若甲同学抽得的数字比乙同学抽得的数字大,甲获胜,反之乙获胜,若数字相同,视为平局.”
(1)请用画树状图或列表的方法计算出平局的概率;
(2)说明这个规则对甲、乙双方是否公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 线段可以比较长短B. 射线可以比较长短
C. 直线可以比较长短D. 直线比射线长
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=﹣3,y=1,则2x﹣y+1的值为( )
A.6B.4C.﹣3D.﹣6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形的上底长是5 cm,下底长是11 cm.当梯形的高由大变小时,梯形的面积也随之发生变化.
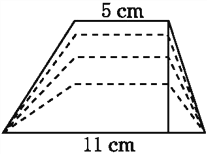
(1)在这个变化过程中,自变量是____________,因变量是____________;
(2)梯形的面积y(cm2)与高x(cm)之间的关系式为____________;
(3)当梯形的高由10 cm变化到1 cm时,梯形的面积由____________变化到____________.
相关试题

