【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx经过两点A(﹣1,1),B(2,2).过点B作BC∥x轴,交抛物线于点C,交y轴于点D.
(1)求此抛物线对应的函数表达式及点C的坐标;
(2)若抛物线上存在点M,使得△BCM的面积为 ![]() ,求出点M的坐标;
,求出点M的坐标;
(3)连接OA、OB、OC、AC,在坐标平面内,求使得△AOC与△OBN相似(边OA与边OB对应)的点N的坐标.
参考答案:
【答案】
(1)
解:把A(﹣1,1),B(2,2)代入y=ax2+bx得: ![]() ,解得
,解得 ![]() ,
,
故抛物线的函数表达式为y= ![]() x2﹣
x2﹣ ![]() x,
x,
∵BC∥x轴,
设C(x0,2).
∴ ![]() x02﹣
x02﹣ ![]() x0=2,解得:x0=﹣
x0=2,解得:x0=﹣ ![]() 或x0=2,
或x0=2,
∵x0<0,
∴C(﹣ ![]() ,2)
,2)
(2)
解:设△BCM边BC上的高为h,
∵BC= ![]() ,
,
∴S△BCM= ![]() h=
h= ![]() ,
,
∴h=2,点M即为抛物线上到BC的距离为2的点,
∴M的纵坐标为0或4,令y= ![]() x2﹣
x2﹣ ![]() x=0,
x=0,
解得:x1=0,x2= ![]() ,
,
∴M1(0,0),M2( ![]() ,0),令y=
,0),令y= ![]() x2﹣
x2﹣ ![]() x=4,
x=4,
解得:x3= ![]() ,x4=
,x4= ![]()
,∴M3( ![]() ,0),M4(
,0),M4( ![]() ,4),
,4),
综上所述:M点的坐标为:(0,0),( ![]() ,0),(
,0),( ![]() ,0),(
,0),( ![]() ,4)
,4)
(3)
解:∵A(﹣1,1),B(2,2),C(﹣ ![]() ,2),D(0,2),
,2),D(0,2),
∴OB=2 ![]() ,OA=
,OA= ![]() ,OC=
,OC= ![]() ,
,
∴∠AOD=∠BOD=45°,tan∠COD= ![]() ,
,
①如图1, 
当△AOC∽△BON时, ![]() ,∠AOC=∠BON,
,∠AOC=∠BON,
∴ON=2OC=5,
过N作NE⊥x轴于E,
∵∠COD=45°﹣∠AOC=45°﹣∠BON=∠NOE,
在Rt△NOE中,tan∠NOE=tan∠COD= ![]() ,
,
∴OE=4,NE=3,
∴N(4,3)同理可得N(3,4);
②如图2, 
当△AOC∽△OBN时, ![]() ,∠AOC=∠OBN,
,∠AOC=∠OBN,
∴BN=2OC=5,
过B作BG⊥x轴于G,过N作x轴的平行线交BG的延长线于F,
∴NF⊥BF,
∵∠COD=45°﹣∠AOC=45°﹣∠OBN=∠NBF,
∴tan∠NBF=tan∠COD= ![]() ,
,
∴BF=4,NF=3,
∴N(﹣1,﹣2),同理N(﹣2,﹣1),
综上所述:使得△AOC与△OBN相似(边OA与边OB对应)的点N的坐标是(4,3),(3,4),(﹣1,﹣2),(﹣2,﹣1).
【解析】(1)把A(﹣1,1),B(2,2)代入y=ax2+bx求得抛物线的函数表达式为y= ![]() x2﹣
x2﹣ ![]() x,由于BC∥x轴,设C(x0 , 2).于是得到方程
x,由于BC∥x轴,设C(x0 , 2).于是得到方程 ![]() x02﹣
x02﹣ ![]() x0=2,即可得到结论;(2)设△BCM边BC上的高为h,根据已知条件得到h=2,点M即为抛物线上到BC的距离为2的点,于是得到M的纵坐标为0或4,令y=
x0=2,即可得到结论;(2)设△BCM边BC上的高为h,根据已知条件得到h=2,点M即为抛物线上到BC的距离为2的点,于是得到M的纵坐标为0或4,令y= ![]() x2﹣
x2﹣ ![]() x=0,或令y=
x=0,或令y= ![]() x2﹣
x2﹣ ![]() x=4,解方程即可得到结论;(3)解直角三角形得到OB=2
x=4,解方程即可得到结论;(3)解直角三角形得到OB=2 ![]() ,OA=
,OA= ![]() ,OC=
,OC= ![]() ,∠AOD=∠BOD=45°,tan∠COD=
,∠AOD=∠BOD=45°,tan∠COD= ![]() ①如图1,当△AOC∽△BON时,求得ON=2OC=5,过N作NE⊥x轴于E,根据三角函数的定义得到OE=4,NE=3,于是得到结果;②如图2,根据相似三角形的性质得到BN=2OC=5,过B作BG⊥x轴于G,过N作x轴的平行线交BG的延长线于F解直角三角形得到BF=4,NF=3于是得到结论.本题主要考查的是二次函数与相似三角形的综合应用,难度较大,解答本题需要同学们熟练掌握二次函数和相似三角形的相关性质.
①如图1,当△AOC∽△BON时,求得ON=2OC=5,过N作NE⊥x轴于E,根据三角函数的定义得到OE=4,NE=3,于是得到结果;②如图2,根据相似三角形的性质得到BN=2OC=5,过B作BG⊥x轴于G,过N作x轴的平行线交BG的延长线于F解直角三角形得到BF=4,NF=3于是得到结论.本题主要考查的是二次函数与相似三角形的综合应用,难度较大,解答本题需要同学们熟练掌握二次函数和相似三角形的相关性质.
【考点精析】本题主要考查了二次函数的性质和相似三角形的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次函数y=ax2+bx+c的图象经过点(﹣2,y1),(﹣1,y2),(1,0),且y1<0<y2 , 对于以下结论:
①abc>0;②a+3b+2c≤0;③对于自变量x的任意一个取值,都有 x2+x≥﹣
x2+x≥﹣  ;④在﹣2<x<﹣1中存在一个实数x0 , 使得x0=﹣
;④在﹣2<x<﹣1中存在一个实数x0 , 使得x0=﹣ 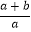 ,
,
其中结论错误的是 (只填写序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=﹣
 x2+bx+c的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
x2+bx+c的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.
(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中,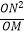 为常数,试确定k的值.
为常数,试确定k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线y=﹣
 x2+
x2+  x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
(1)判断△ABC的形状,并说明理由;
(2)经过B,C两点的直线交抛物线的对称轴于点D,点P为直线BC上方抛物线上的一动点,当△PCD的面积最大时,Q从点P出发,先沿适当的路径运动到抛物线的对称轴上点M处,再沿垂直于抛物线对称轴的方向运动到y轴上的点N处,最后沿适当的路径运动到点A处停止.当点Q的运动路径最短时,求点N的坐标及点Q经过的最短路径的长;
(3)如图2,平移抛物线,使抛物线的顶点E在射线AE上移动,点E平移后的对应点为点E′,点A的对应点为点A′,将△AOC绕点O顺时针旋转至△A1OC1的位置,点A,C的对应点分别为点A1 , C1 , 且点A1恰好落在AC上,连接C1A′,C1E′,△A′C1E′是否能为等腰三角形?若能,请求出所有符合条件的点E′的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )

A.
B.
C.
D.
相关试题

