【题目】猜想:当点E在两条直线AB,CD之外时(如图1和2),∠BED,∠B,∠D满足怎样的关系时,有AB∥CD?对猜想进行证明.

参考答案:
【答案】(1)当∠B=∠BED+∠D时,有AB∥CD.证明见解析;(2)当∠B=∠BED+∠D时,有AB∥CD.证明见解析.
【解析】
(1)过点E作EF∥AB,由∠B=∠BED+∠D,结合题意,得到AB∥CD;
(2)设BE与CD交于点O.结合题意推得∠BOD=∠B,从而得到AB∥CD.
(1)当∠B=∠BED+∠D时,有AB∥CD.证明如下:
如图1,过点E作EF∥AB,则∠B+∠FEB=180°,
∵∠B=∠BED+∠D,
∴∠FEB+∠BED+∠D=180°,
∴EF∥CD,
∴AB∥CD;
(2)当∠B=∠BED+∠D时,有AB∥CD.证明如下:
如图2,设BE与CD交于点O.
∵∠BOD=∠BED+∠D,∠B=∠BED+∠D,
∴∠BOD=∠B,
∴AB∥CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在梯形ABCD中,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.
求证:CE⊥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
 中,
中, ,
, ,点
,点 在
在 边上以每秒
边上以每秒 的速度从点
的速度从点 向点
向点 运动,点
运动,点 在
在 边上,以每秒
边上,以每秒 的速度从点
的速度从点 出发,在
出发,在 间往返运动,两个点同时出发,当点
间往返运动,两个点同时出发,当点 到达点
到达点 时停止(同时点
时停止(同时点 也停止).设运动时间为
也停止).设运动时间为 秒,当
秒,当 为何值时,以点
为何值时,以点 、
、 、
、 、
、 为顶点的四边形是平行四边形?
为顶点的四边形是平行四边形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条长为60 cm的卷尺铺平后折叠,使得卷尺自身的一部分重合,然后在重合部分(阴影处)沿与卷尺边垂直的方向剪一刀,此时卷尺分成了三段,若这三段长度由短到长的比为1∶2∶3,则折痕对应的刻度有________种可能.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )

A.18B.20C.22D.24
-
科目: 来源: 题型:
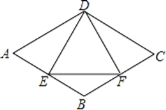
查看答案和解析>>【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
A.3
B.4
C.1
D.2
相关试题

