【题目】如图,EF∥AD,∠1=∠2.证明:∠DGA+∠BAC=180°.请完成说明过程.
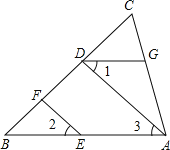
解:∵EF∥AD,(已知)
∴∠2=∠3.( )
又∵∠1=∠2(已知)
∴∠1=∠3,(等量代换)
∴AB∥ ,( )
∴∠DGA+∠BAC=180°.( )
参考答案:
【答案】两直线平行,同位角相等;DG;内错角相等,两直线平行;两直线平行,同旁内角互补.
【解析】
先利用平行线的性质由EF∥AD得到∠2=∠3,再利用等量代换得到∠1=∠3,则根据平行线的判定判断AB∥DG,然后根据平行线的性质得到∠DGA+∠BAC=180°.
解:∵EF∥AD,(已知)
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠1=∠3,(等量代换)
∴AB∥DG,(内错角相等,两直线平行)
∴∠DGA+∠BAC=180°.(两直线平行,同旁内角互补).
故答案为:两直线平行,同位角相等;DG;内错角相等,两直线平行;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A. 对我市市民实施低碳生活情况的调查
B. 对我国首架大型民用飞机零部件的检查
C. 对全国中学生心理健康现状的调查
D. 对市场上的冰淇淋质量的调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣3x+k与x轴交于A、B两点,与y轴交于点C(0,﹣4).

(1)k=;
(2)点A的坐标为 , B的坐标为;
(3)设抛物线y=x2﹣3x+k的顶点为M,求四边形ABMC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图. 根据上述信息,解答下列问题:

(1)本次抽取的学生人数是 ;扇形统计图中的圆心角α等于 ;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+
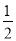 ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
A. ①② B. ③④ C. ①②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的面积为8cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )

A. 2cm2 B. 3cm2 C. 4cm2 D. 5cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边三角形ABC的边长为3,过AB边上一点P作PE
 AC于点E,Q为BC延长线上一点,取PA=CQ,连接PQ,交AC于M,则EM的长为_________________.
AC于点E,Q为BC延长线上一点,取PA=CQ,连接PQ,交AC于M,则EM的长为_________________.
相关试题

