【题目】如图,在平面直角坐标系xOy中,△OAB如图放置,点A的坐标为(3,4),点P是AB边上的一点,过点P的反比例函数 ![]() 与OA边交于点E,连接OP.
与OA边交于点E,连接OP.
(1)如图1,若点B的坐标为(5,0),且△OPB的面积为 ![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(2)如图2,过P作PC∥OA,与OB交于点C,若 ![]() ,并且△OPC的面积为
,并且△OPC的面积为 ![]() ,求OE的长.
,求OE的长.
参考答案:
【答案】
(1)
解:如图1中,过点P作PD⊥OB于点D,
∵点B的坐标为(5,0),
△OPB的面积为 ![]() ,
,
∴ ![]() ×5PD=
×5PD= ![]() ,解得PD=1,
,解得PD=1,
设直线AB的解析式为
y=ax+b(a≠0),
∵A(3,4),B(5,0),
∴ ![]() ,解得
,解得 ![]() ,
,
∴直线AB的解析式为y=﹣2x+10,
当y=1时,﹣2x+10=1,解得x= ![]() ,
,
∴P( ![]() ,1),
,1),
∵点P的反比例函数y= ![]() (x>0)上,
(x>0)上,
∴1= ![]() ,解得k=
,解得k= ![]() ,
,
∴反比例函数的解析式为:y= ![]() ;
;

(2)
解:如图2中,作PN⊥OB于N,AH⊥OB于H,EM⊥OB于M.
∵PC∥OA,
∴∠PCN=∠AOH,∵∠AHO=∠PNC,
∴△AHO∽△PNC,同理△EMO∽△PNC,
∵AO:AH:OH=5:4:3,
∴PC:PN:CN=5:4:3,设点点P坐标(m,4n),则CN=3n,PC=5n,
∵△EMO∽△ONC,OE=2PC,
∴EM=8n,OM=6n,E(6n,8n)
∴6n8n=m4n,
∴m=12n,
∵S△POC= ![]() ,
,
∴ ![]() (12n﹣3n)4n=
(12n﹣3n)4n= ![]() ,
,
∴n= ![]() (负根已经舍弃).
(负根已经舍弃).
∴点E坐标( ![]() ,
, ![]() ),
),
∴OE= ![]() .
.

【解析】(1)过点P作PD⊥OB于点D,根据点B的坐标为(5,0),且△OPB的面积为 ![]() 求出PD的长,求出直线AB的解析式,故可得出P点坐标,利用待定系数法求出反比例函数的解析式即可;(2)如图2中,作PN⊥OB于N,AH⊥OB于H,EM⊥OB于M,由△AHO∽△PNC,△EMO∽△PNC,因为AO:AH:OH=5:4:3,所以PC:PN:CN=5:4:3,设点点P坐标(m,4n),则CN=3n,PC=5n,列方程求出n,m即可解决问题.
求出PD的长,求出直线AB的解析式,故可得出P点坐标,利用待定系数法求出反比例函数的解析式即可;(2)如图2中,作PN⊥OB于N,AH⊥OB于H,EM⊥OB于M,由△AHO∽△PNC,△EMO∽△PNC,因为AO:AH:OH=5:4:3,所以PC:PN:CN=5:4:3,设点点P坐标(m,4n),则CN=3n,PC=5n,列方程求出n,m即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
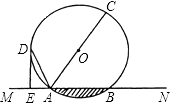
(1)求证:DE是⊙O的切线;
(2)若DE=6,AE= ,求⊙O的半径;
,求⊙O的半径;
(3)在第(2)小题的条件下,则图中阴影部分的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】大润发超市进了一批成本为8元/个的文具盒.调查发现:这种文具盒每个星期的销售量y(个)与它的定价x(元/个)的关系如图所示:

(1)求这种文具盒每个星期的销售量y(个)与它的定价x(元/个)之间的函数关系式(不必写出自变量x的取值范围);
(2)每个文具盒的定价是多少元时,超市每星期销售这种文具盒(不考虑其他因素)可获得的利润为1200元?
(3)若该超市每星期销售这种文具盒的销售量不少于115个,且单件利润不低于4元(x为整数),当每个文具盒定价多少元时,超市每星期利润最高?最高利润是多少? -
科目: 来源: 题型:
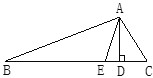
查看答案和解析>>【题目】已知,如图,在△ ABC中,AD,AE分别是 △ ABC的高和角平分线,若∠B=30°,∠C=50°.
(1)求∠DAE的度数.
(2)试写出 ∠DAE与∠C-∠B有何关系?(不必证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)作出符合本题的几何图形;
(2)求证:BE∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=
 ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.

相关试题

