搜索
【题目】如图，某沿海城市A接到台风警报，在该城市正南方向260 km的B处有一台风中心，沿BC方向以15 km/h的速度向C移动，已知城市A到BC的距离AD＝100 km，那么台风中心经过多长时间从B点移动到D点？如果在距台风中心30 km的圆形区域内都将受到台风的影响，正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响？
参考答案：
【答案】在接到台风警报后的14 h内撤离才可以免受台风的影响．
【解析】
首先根据勾股定理计算BD的长，再根据时间=路程÷速度计算从B点移动到D点所用时间；根据在30千米范围内都要受到影响，先求出从点B到受影响的距离与结束影响的距离，再根据时间=路程÷速度计算，然后求出时间段即可．
根据题意，画图得：
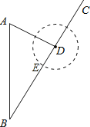
在Rt△ABD中，∵AB＝260 km，AD＝100 km，
∴台风中心从B点移动到D点所用的时间为
在D点休息的游人应在台风中心距D点30 km前撤离，30÷15＝2(h)，16－2＝14(h)．
答：在接到台风警报后的14 h内撤离才可以免受台风的影响．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若a，b，c是直角三角形的三条边长(c为斜边长)，斜边上的高是h，给出下列结论：
①长为a2，b2，c2的三条线段能组成一个三角形；②长为
，
，
的三条线段能组成一个三角形；③长为a＋b，c＋h，h的三条线段能组成直角三角形；④长为
，
，
的三条线段能组成直角三角形．其中所有正确结论的序号为__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，CD⊥AB ， 垂足为D ， AB=c ， ∠a=α ， 则CD长为（ ）
A.csin2α
B.ccos2α
C.csinαtanα
D.csinαcosα -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在△ABC中，AB:BC:CA=3:4:5，且周长为36cm，点P从点A开始沿AB边向点B以每秒1cm的速度移动；点Q从点B沿BC边向点C以每秒2cm的速度移动；如果同时出发，则过3秒时，求△BPQ的面积。
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景
在△ABC中，AB，BC，AC的长分别为
，
，
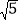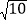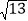，求这个三角形的面积．晓辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点三角形ABC(即△ABC的三个顶点都在小正方形的顶点处)，如图①所示，这样不需求△ABC的高，而借用网格就能计算出它的面积．(1)请你直接写出△ABC的面积：________.
(2)我们把上述求△ABC面积的方法叫做构图法．若△ABC的三边长分别为
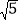a，2
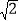a，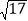
a(a>0)，请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC，并求出它的面积．探索创新
(3)若△ABC的三边长分别为
，
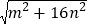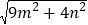，2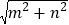
(m>0，n>0，且m≠n)，试运用构图法(自己重新设计一个符合结构特征的网格)求出这个三角形的面积．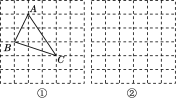
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学活动课上，小敏.小颖分别画了△ABC和△DEF ， 尺寸如图 ． 如果两个三角形的面积分别记作S△ABC.S△DEF ， 那么它们的大小关系是（ ）
A.S△ABC＞S△DEF
B.S△ABC＜S△DEF
C.S△ABC=S△DEF
D.不能确定 -
科目： 来源： 题型：
查看答案和解析>>【题目】数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A.B的距离，他们设计了如图所示的测量方案：从树A沿着垂直于AB的方向走到E ， 再从E沿着垂直于AE的方向走到F ， C为AE上一点，其中3位同学分别测得三组数据：①AC ， ∠ACB；②EF.DE.AD；③CD ， ∠ACB ， ∠ADB.其中能根据所测数据求得A.B两树距离的有（ ）
A.0组
B.一组
C.二组
D.三组
相关试题
