【题目】(1)观察发现:如图1,已知Rt△ABC,∠ABC=90°,分别以AB,BC为边,向外作正方形ABDE和正方形BCFG,连接DG.若M是DG的中点,不难发现:BM=![]() AC.
AC.
请完善下面证明思路:①先根据 ,证明BM=![]() DG;②再证明 ,得到DG=AC;所以BM=
DG;②再证明 ,得到DG=AC;所以BM=![]() AC;
AC;
(2)数学思考:若将上题的条件改为:“已知Rt△ABC,∠ABC=90°,分别以AB,AC为边向外作正方形ABDE和正方形ACHI,N是EI的中点”,则相应的结论“AN=![]() BC”成立吗?
BC”成立吗?
小颖通过添加如图2所示的辅助线验证了结论的正确性.请写出小颖所添加的辅助线的作法,并由此证明该结论;
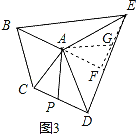
(3)拓展延伸:如图3,已知等腰△ABC和等腰△ADE,AB=AC,AD=AE.连接BE,CD,若P是CD的中点,探索:当∠BAC与∠DAE满足什么条件时,AP=![]() BE,并简要说明证明思路.
BE,并简要说明证明思路.

参考答案:
【答案】(1)直角三角形斜边上的中线等于斜边的一半,△BDG≌△BAC;(2)能,理由见解析;(3)当∠BAC=∠DAE=90°时,AP=![]() BE,
BE,
【解析】试题分析:(1)根据题意即可得到结论;
(2)过I作IK⊥EA交EA的延长线于K,根据平角的定义得到∠BAC=∠IAK,根据全等三角形的性质得到BC=IK,AB=AK,等量代换得到AE=AI,推出AN是△EKI的中位线,于是得到结论.
(3)延长BA到F,使AF=AB,连接EF,过A作AG∥BE,根据三角形中位线的性质得到AG=![]() BE,根据全等三角形的性质得到∠ADC=∠AEF,EF=CD,根据全等三角形的性质即可得到结论.
BE,根据全等三角形的性质得到∠ADC=∠AEF,EF=CD,根据全等三角形的性质即可得到结论.
试题解析:
(1)①直角三角形斜边上的中线等于斜边的一半,②△BDG≌△BAC;
故答案为:直角三角形斜边上的中线等于斜边的一半,△BDG≌△BAC;
(2)能,
理由:过I作IK⊥EA交EA的延长线于K,
∵∠EAI+∠BAC=360°﹣90°﹣90°=180°,∠EAI+∠TAK=180°,
∵∠BAC=∠IAK,
在△ABC与△AKI中, ,
,
∴△ABC≌△AKI,
∴BC=IK,AB=AK,
∵AE=AB,
∴AE=AI,
∵N是EI的中点,
∴AN是△EKI的中位线,
∴AN=![]() IK,
IK,
∴AN=![]() BC;
BC;
(3)当∠BAC=∠DAE=90°时,AP=![]() BE,
BE,
延长BA到F,使AF=AB,连接EF,过A作AG∥BE,
∴EG=![]() EF,
EF,
∴AG=![]() BE,
BE,
∵∠BAC=∠DAE=90°,
∴∠CAD=180°﹣∠BAE,
∵∠FAE=180°﹣BAE,
∴∠CAD=∠FAE,
在△ACD与△AFE中, ,
,
∴△ACD≌△FAE,
∴∠ADC=∠AEF,EF=CD,
∵P是CD的中点,
∴DP=![]() CD,
CD,
∴EG=DP,
在△ADP与△AEG中,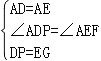 ,
,
∴△ADP≌△AEG,
∴AP=AG,
∴AP=![]() BE.
BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四个完全相同的小球上分别标上1,2,3,4四个数字,然后装入一个不透明的口袋里搅匀,小明同学随机摸取一个小球记下标号,然后放回,再随机摸取一个小球,记下标号.
(1)请你用画树状图或列表的方法分别表示小明同学摸球的所有可能出现的结果.
(2)按照小明同学的摸球方法,把第一次取出的小球的数字作为点M的横坐标,把第二次取出的小球的数字作为点M的纵坐标,试求出点M(x,y)落在直线y=x上的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级举行“生活中的数学”数学小论文比赛活动,购买A、B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元,根据比赛设奖情况,需要购买两种笔记本共30本,若学校决定购买本次笔记本所需资金不能超过280元,设买A种笔记本x本.
(1)根据题意完成以下表格(用含x的代数式表示)
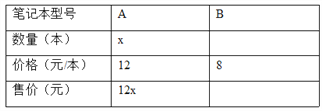
(2)那么最多能购买A笔记本多少本?
(3)若购买B笔记本的数量要小于A笔记本的数量的3倍,则购买这两种笔记本各多少本时,费用最少,最少的费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:3,4,5,5,6,6,6,这组数据的众数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某蛋白质分子的直径是0.00000043米,用科学记数法表示为( )
A.4.3×107米B.﹣4.3×107米
C.4.3×10﹣7米D.0.43×10﹣6米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个数的绝对值等于这个数的相反数,那么这个数一定是( )
A. 正数 B. 负数 C. 非正数 D. 非负数
相关试题

