【题目】如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线上绕其右下角的顶点B向右旋转90°
至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置……以此类推,这样连续旋转2018
次后,顶点A在整个旋转过程中所经过的路线之和是_________

参考答案:
【答案】6057![]()
【解析】解:在矩形ABCD中,AB=8,BC=6,∴AC=BD=10,转动一次A的路线长是: ![]() =4π,转动第二次的路线长是:
=4π,转动第二次的路线长是: ![]() =5π,转动第三次的路线长是:
=5π,转动第三次的路线长是: ![]() =3π,转动第四次的路线长是:0,以此类推,每四次循环,故顶点A转动四次经过的路线长为:4π+5π+3π=12π,2018÷4=504余2,顶点A在整个旋转过程中所经过的路线之和为:12π×504+4π+5π=6057π.故答案为:6057π.
=3π,转动第四次的路线长是:0,以此类推,每四次循环,故顶点A转动四次经过的路线长为:4π+5π+3π=12π,2018÷4=504余2,顶点A在整个旋转过程中所经过的路线之和为:12π×504+4π+5π=6057π.故答案为:6057π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,
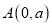 、
、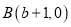 ,且
,且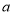 、
、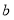 满足
满足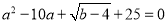
(1)求
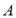 、
、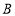 两点的坐标;
两点的坐标;(2)过点
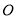 的直线
的直线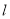 上有一点
上有一点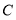 ,连接
,连接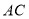 、
、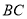 ,
,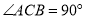 ,如图2,当点
,如图2,当点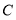 在第二象限时,
在第二象限时,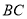 交
交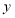 轴于点
轴于点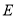 ,延长
,延长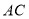 交
交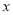 轴于点
轴于点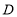 ,设
,设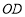 的长为
的长为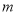 ,
,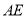 的长为
的长为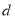 ,用含
,用含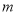 的式子表示
的式子表示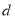 ;
;(3)在(2)的条件下,如图3,当点
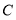 在第一象限时,过点
在第一象限时,过点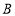 作
作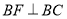 交
交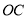 于点
于点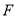 ,连接
,连接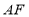 ,若
,若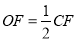 ,
,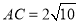 ,求
,求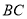 的长.
的长.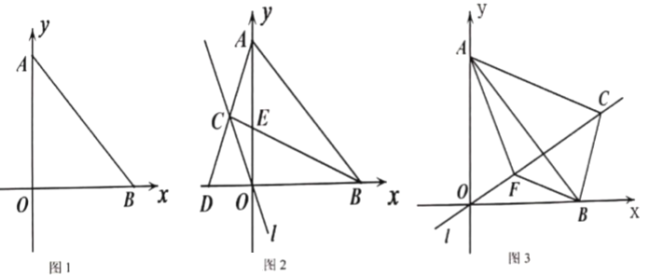
-
科目: 来源: 题型:
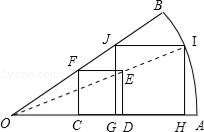
查看答案和解析>>【题目】小明手上一张扇形纸片OAB.现要求在纸片上截一个正方形,使它的面积尽可能大.
小明的方案是:如图,在扇形纸片OAB内,画正方形CDEF,使C、D在OA上,F在OB上;连接OE并延长交弧AB于I,画IH∥ED交OA于H,IJ∥OA交OB于J,再画JG∥FC交OA于G.
(1)你认为小明画出的四边形GHIJ是正方形吗?如果是,请证明.如果不是,请说明理由.
(2)如果扇形OAB的圆心角∠AOB=30°,OA=6cm,小明截得的四边形GHIJ面积是多少(结果精确到0.1cm).
(3)(1)中小明画出的四边形GHIJ如果是正方形,我们把它叫做扇形的内接正方形(四个顶点分别在扇形的半径和弧上).请你再画出一种不同于图(1)的扇形的内接正方形(保留画图痕迹,不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用两种正多边形铺满地面,其中一种是正八边形,则另一种正多边形是( )。
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个8×10的网格,每个小正方形的顶点叫格点,每个小正方形的边长均为1,△ABC的顶点均在格点上.
(1)画出△ABC关于直线OM对称的图形△
 .
.(2)画出△ABC关于点O的中心对称图形 △
 .
.(3)△
 与△
与△ 组成的图形__________ 轴对称图形. (填“是”或“不是”)
组成的图形__________ 轴对称图形. (填“是”或“不是”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD 是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC
(1)求∠OCA的度数 (2)如果OE
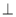 AC于F,且OC=
AC于F,且OC=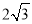 , 求AC的长
, 求AC的长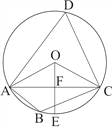
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
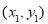 ,
,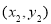 均在双曲线
均在双曲线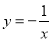 上,下列说法中错误的是( )
上,下列说法中错误的是( )A.若
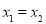 ,则
,则 B.若
B.若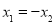 ,则
,则
C.若
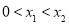 ,则
,则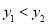 D.若
D.若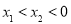 ,则
,则
相关试题

