【题目】阅读下列材料并解决有关问题:我们知道|x|=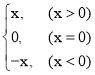 ,现在我们可以用这个结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别叫做|x+1|与|x﹣2|的零点值.)在有理数范围内,零点值x=﹣1和x=2可将全体有理数分成不重复且不遗漏的如下3种情况:
,现在我们可以用这个结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别叫做|x+1|与|x﹣2|的零点值.)在有理数范围内,零点值x=﹣1和x=2可将全体有理数分成不重复且不遗漏的如下3种情况:
(1)当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
(2)当﹣1≤x≤2时,原式=x+1﹣(x﹣2)=3;
(3)当x>2时,原式=x+1+x﹣2=2x﹣1.
综上所述,原式=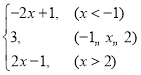 .
.
通过以上阅读,请你解决以下问题:
(1)分别求出|x+2|和|x﹣4|的零点值;
(2)化简代数式|x+2|+|x﹣4|;
(3)求方程:|x+2|+|x﹣4|=6的整数解;
(4)|x+2|+|x﹣4|是否有最小值?如果有,请直接写出最小值;如果没有,请说明理由.
参考答案:
【答案】(1)﹣2,4分别为|x+2|和|x﹣4|的零点值;(2)当x<﹣2时,﹣2x+2;当﹣2≤x<4时, 6;当x≥4时, 2x﹣2;(3)整数解为:﹣2,﹣1,0,1,2,3,4;(4)有,|x+2|+|x﹣4|的最小值是6.
【解析】
(1)根据题中所给材料,求出零点值;
(2)将全体实数分成不重复且不遗漏的三种情况解答;
(3)由|x+2|+|x-4|=6,得到-2≤x≤4,于是得到结果;
(4)|x+2|+|x-4|有最小值,通过x的取值范围即可得到结果.
(1)∵|x+2|和|x﹣4|的零点值,可令x+2=0和x﹣4=0,解得x=﹣2和x=4,
∴﹣2,4分别为|x+2|和|x﹣4|的零点值.
(2)当x<﹣2时,|x+2|+|x﹣4|=﹣2x+2;
当﹣2≤x<4时,|x+2|+|x﹣4|=6;
当x≥4时,|x+2|+|x﹣4|=2x﹣2;
(3)∵|x+2|+|x﹣4|=6,
∴﹣2≤x≤4,
∴整数解为:﹣2,﹣1,0,1,2,3,4.
(4)|x+2|+|x﹣4|有最小值,
∵当x=﹣2时,|x+2|+|x﹣4|=6,
当x=4时,|x+2|+|x﹣4|=6,
∴|x+2|+|x﹣4|的最小值是6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:b是最小的正整数,且a、b满足(c﹣6)2+|a+b|=0,请回答问题
(1)请直接写出a、b、c的值.a= ,b= ,c=
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在A、B之间运动时,请化简式子:|x+1|﹣|x﹣1|﹣2|x+5|(请写出化简过程)
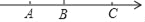
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒n(n>0)个单位长度的速度向左运动,同时,点B和点C分别以每秒2n个单位长度和5n个单位长度的速度向右运动,假设经过t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
-
科目: 来源: 题型:
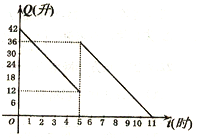
查看答案和解析>>【题目】某机动车出发前油箱内有42升油,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图,回答下列问题(1)机动车行驶________小时后加油,中途加油_______升;(2)求加油前油箱剩余油量Q与行驶时间t的函数关系,并直接写出自变量t的取值范围;(3)如果加油站距目的地还有230千米,车速为40千米/时,要到达目的地,油箱中的油是否够用?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】滴滴打车为市民的出行带来了很大的方便,小亮调查了若干市民一周内使用滴滴打车的时间t(单位:分),将获得的数据分成四组,绘制了如下统计图,请根据图中信息,解答下列问题:
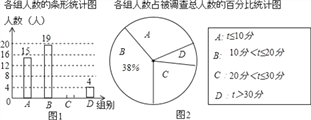
(1)这次被调查的总人数是多少?
(2)试求表示C组的扇形圆心角的度数,并补全条形统计图;
(3)若全市的总人数为666万,试求全市一周内使用滴滴打车超过20分钟的人数大约有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据3,4,4,5,若添加一个数4,则发生变化的统计量是( )
A.平均数B.众数C.中位数D.方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角三角形EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤
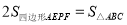 ,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合)上述结论正确的是_____________.(填序号)
,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合)上述结论正确的是_____________.(填序号)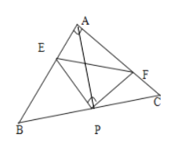
-
科目: 来源: 题型:
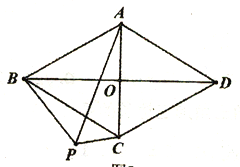
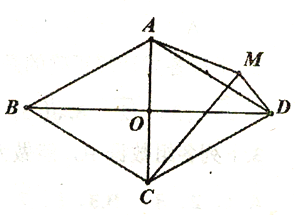
查看答案和解析>>【题目】已知在菱形ABCD中,对角线AC、BD交于点O,AB=2AO;(1)如图1,求∠BAC的度数;(2)如图2,P为菱形ABCD外一点,连接AP、BP、CP,若∠CPB=120°,求证:CP+BP=AP;(3)如图3,M为菱形ABCD外一点,连接AM、CM、DM,若∠AMD=150°,
CM=2
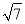 ,DM=2,求四边形ACDM的面积。
,DM=2,求四边形ACDM的面积。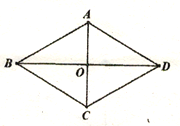
相关试题

