【题目】如图，正比例函数y=2x的图象与反比例函数y= k x 的图象交于A、B两点，过点A作AC垂直x轴于点C，连结BC．若△ABC的面积为2．

（1）求k的值；
（2）利用图象求出不等式2x＞ 的解集．

参考答案：

【答案】
（1）

解：设点A的坐标为（m，n）．

∵点A在直线y=2x上，∴n=2m．

根据对称性可得OA=OB，

∴S△ABC=2S△ACO=2，

∴S△ACO=1，

∴ m2m=1，

∴m=1（舍负），

∴点A的坐标为（1，2），

∴k=1×2=2；


（2）

解：如图，

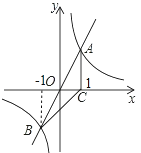
由点A与点B关于点O成中心对称得点B（﹣1，﹣2）．

结合图象可得：不等式2x＞ 的解集为x＞1或﹣1＜x＜0

；

解：如图，

由点A与点B关于点O成中心对称得点B（﹣1，﹣2）．

结合图象可得：不等式2x＞ 的解集为x＞1或﹣1＜x＜0

；
；

解：如图，

由点A与点B关于点O成中心对称得点B（﹣1，﹣2）．

结合图象可得：不等式2x＞ 的解集为x＞1或﹣1＜x＜0
【解析】（1）根据对称性可得OA=OB，从而可得△ACO的面积为1，由此可求出点A的坐标，然后运用待定系数法就可解决问题；（2）只需求出点B的坐标，并运用数形结合的思想就可解决问题．

关闭