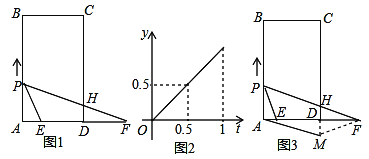
【题目】如图1,矩形ABCD中,AB=7cm,AD=4cm,点E为AD上一定点,F为AD延长线上一点,且DF=acm,点P从A点出发,沿AB边向点B以2cm/s的速度运动,运动到B点停止,连结PE,设点P运动的时间为ts,△PAE的面积为ycm2,当0≤t≤1时,△PAE的面积y(cm2)关于时间t(s)的函数图象如图2所示,连结PF,交CD于点H.
(1)t的取值范围为 ,AE cm;
(2)如图3,将△HDF沿线段DF进行翻折,与CD的延长线交于点M,连结AM,当a为何值时,四边形PAMH为菱形?
(3)在(2)的条件下求出点P的运动时间t.
参考答案:
【答案】(1)0≤t≤3.5,AE=1;
(2)a=4;
(3)P的运动时间为=![]() 秒.
秒.
【解析】证明:(1)∵AB=7,7÷2=3.5,
∴0≤t≤3.5,由题意可知y=![]() ×2t×AE,
×2t×AE,
∴由图象可知t=0.5时,y=0.5,
∴0.5=![]() ×2×0.5×AE,
×2×0.5×AE,
∴AE=1,
故答案分别为0≤t≤3.5,AE=1.
(2)如图3中,∵四边形AMHP是菱形,
∴AM=MH=2DM,AM∥PF,
∵∠ADM=90,∴∠MAD=30,
∴∠PFA=MFA=∠MAD=30,∴MA=MF,∵MD⊥AF,
∴AD=DF=4,∴a=4.
(3)∴当a=4cm时,此时FA=8cm,令PA=x,则PF=2x,根据勾股定理可得,PF2=PA2+AF2,
则(2x)2= x2+82,
解得x=![]() ,
,
∴P的运动时间为![]() ÷2=
÷2=![]() 秒.
秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程x2+4xy﹣5y2=0化为两个二元一次方程,它们是_____和_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断错误的是( )
A. 一个正数的绝对值一定是正数; B. 一个负数的绝对值一定是正数;
C. 任何数的绝对值一定是正数; D. 任何数的绝对值都不是负数;
-
科目: 来源: 题型:
查看答案和解析>>【题目】0.49的算术平方根的相反数是( )
A. 0.7 B. -0.7 C. ±0.7 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张)
零售价(元/张)
成套售价(元/套)
餐桌
a
270
500元
餐椅
a﹣110
70
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,按照(2)中获得最大利润的方案购进餐桌和餐椅,在调整成套销售量而不改变销售价格的情况下,实际全部售出后,所得利润比(2)中的最大利润少了2250元.请问本次成套的销售量为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有学生2100人,在“文明我先行”的活动中,开设了“法律、礼仪、感恩、环保、互助”五门校本课程,规定每位学生必须且只能选择一门。为了解学生的报名意向学校随机调查了100名学生,并制成如下统计表:
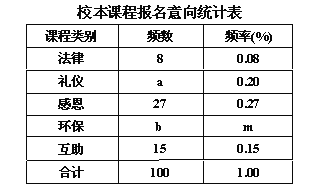
(1)在这次调查活动中,学校采取的调查的方式是 (填写“普查”或“抽样调查”)
(2)a= ,b= ,m= .
(3)如果要画“校本课程报名意向扇形统计图”,那么“礼仪”类校本课程所对应的扇形圆心角的度数是 .
(4)请你统计,全校选择“环保”类校本课程的学生约有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小文在甲、乙两家超市发现他看中的篮球的单价相同,书包单价也相同,一个篮球和三个书包的总费用是400元.两个篮球和一个书包的总费用也是400元.
(1)求小文看中的篮球和书包单价各是多少元?
(2)某一天小文上街,恰好赶上商家促销,超市甲所有商品打九折销售,超市乙全场购物满100元返30元购物券(不足100元不返券,购物券全场通用),如果他只能在同一家超市购买他看中的篮球和书包各一个,应选择哪一家超市购买更省钱?并说明理由.
相关试题

