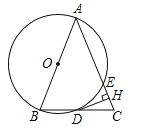
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:H为CE的中点;
(3)若BC=10,cosC=![]() ,求AE的长.
,求AE的长.
参考答案:
【答案】(1)相切;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)连结OD、AD,如图,先利用圆周角定理得到∠ADB=90°,则根据等腰三角形的性质得BD=CD,再证明OD为△ABC的中位线得到OD∥AC,加上DH⊥AC,所以OD⊥DH,然后根据切线的判定定理可判断DH为⊙O的切线;
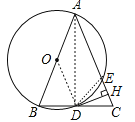
(2)连结DE,如图,有圆内接四边形的性质得∠DEC=∠B,再证明∠DEC=∠C,然后根据等腰三角形的性质得到CH=EH;
(3)利用余弦的定义,在Rt△ADC中可计算出AC=![]() ,在Rt△CDH中可计算出CH=
,在Rt△CDH中可计算出CH=![]() ,则CE=2CH=
,则CE=2CH=![]() ,然后计算AC﹣CE即可得到AE的长.
,然后计算AC﹣CE即可得到AE的长.
试题解析:(1)DH与⊙O相切.理由如下:
连结OD、AD,如图,∵AB为直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴BD=CD,而AO=BO,∴OD为△ABC的中位线,∴OD∥AC,∵DH⊥AC,∴OD⊥DH,∴DH为⊙O的切线;
(2)证明:连结DE,如图,∵四边形ABDE为⊙O的内接四边形,∴∠DEC=∠B,∵AB=AC,∴∠B=∠C,∴∠DEC=∠C,∵DH⊥CE,∴CH=EH,即H为CE的中点;
(3)解:在Rt△ADC中,CD=![]() BC=5,∵cosC=
BC=5,∵cosC=![]() =
=![]() ,∴AC=
,∴AC=![]() ,在Rt△CDH中,∵cosC=
,在Rt△CDH中,∵cosC=![]() =
=![]() ,∴CH=
,∴CH=![]() ,∴CE=2CH=
,∴CE=2CH=![]() ,∴AE=AC﹣CE=
,∴AE=AC﹣CE=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x1,x2是方程x2﹣x﹣1=0的两根,则x12+x22的值是( )
A. 3 B. 1 C. ﹣1 D. ﹣3
-
科目: 来源: 题型:
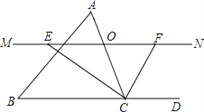
查看答案和解析>>【题目】如图,在△ABC中,点O是边AC上一个动点(不与点A、C重合),过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)探究OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动到什么位置,四边形AECF是矩形,请说明理由;
(3)在第(2)问的基础上,△ABC满足什么条件时,四边形AECF是正方形?(不需说明理由)
(4)当点O在边AC上运动时,四边形BCFE能成为菱形吗?若能,请加以证明;若不能,则说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.在-6、-2、0、3这四个数中,最小的数是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果盈利700元记为+700元,那么亏损300元记为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(m﹣1)x2+2mx﹣3=0是一元二次方程,则m的取值是( )
A. 任意实数 B. m≠1 C. m≠﹣1 D. m>1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在落实国家“营养餐”工程中,选用了A,B,C,D种不同类型的套餐.实行一段时间后,学校决定在全校范围内随机抽取部分学生对“你喜欢的套餐类型(必选且只选一种)”进行问卷调查,将调查情况整理后,绘制成如图所示的两个统计图.

请你根据以上信息解答下列问题:
(1)在这次调查中,一共抽取了 名学生;
(2)请补全条形统计图;
(3)如果全校有1200名学生,请你估计其中喜欢D套餐的学生的人数.
相关试题

