搜索
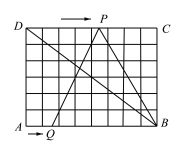
【题目】如图，在6×8的网格纸中，每个小正方形的边长都为1，动点P、Q分别从点D、A同时出发向右移动，点P的运动速度为每秒2个单位，点Q的运动速度为每秒1个单位，当点P运动到点C时，两个点都停止运动.运动时间t 为_______秒时，△PQB成为以PQ为腰的等腰三角形.
参考答案：
【答案】
或
【解析】
作QS⊥FE于S， △PQB是以PQ为腰的等腰三角形分以下两种情况分别求解，①当PB=PQ时，由
；②当QB=QP时，
QB=8-t，求解即可
解：如图：作QS⊥FE于S
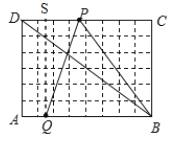
由题意得：PD=2t，AQ=t，则PS=2t-t=t
在Rt△PSQ中，
，
∴
①当PB=PQ时，；
解得：t=或8（舍去）
②当QB=QP时，
解得：t=
故运动时间为或秒时，△PQB是以PQ为腰的等腰三角形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司有2位股东，25名工人，从2006年至2008年，公司每年股东的总利润和每年工人的工资总额如图所示．
（1）填写下表
年份
2006年
2007年
2008年
工人的平均工资/元
股东的平均工资/元
（2）假设在以后的若干年中，每年工人的工资和股东的利润都按图中的速度增长，那么到哪一年，股东的平均利润是工人的平均工资的10倍？
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的口袋里装有分别标有汉字“书”、“ 香”、“ 历”、“ 城”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀．
（1）若从中任取一个球，球上的汉字刚好是 “书”的概率为__________.
（2）从中任取一球，不放回，再从中任取一球，请用树状图或列表的方法，求取出的两个球上的汉字能组成“历城”的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：
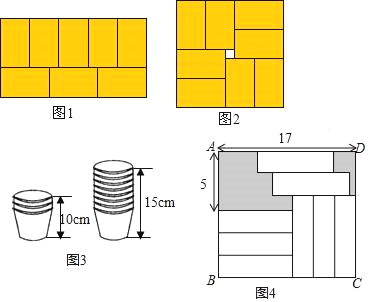
小明是个爱动脑筋的学生，他在学习了二元一次方程组后遇到了这样一道题目：现有8个大小相同的长方形，可拼成如图1、2所示的图形，在拼图②时，中间留下了一个边长为2的小正方形，求每个小长方形的面积．
小明设小长方形的长为x，宽为y，观察图形得出关于x、y的二元一次方程组，解出x、y的值，再根据长方形的面积公式得出每个小长方形的面积．
解决问题：
（1）请按照小明的思路完成上述问题：求每个小长方形的面积；
（2）某周末上午，小明在超市帮妈妈买回一袋纸杯，他把纸杯整齐地叠放在一起，如图3所示．若小明把13个纸杯整齐叠放在一起时，它的高度约是 cm；
（3）小明进行自主拓展学习时遇到了以下这道题目：如图，长方形ABCD中放置8个形状、大小都相同的小长方形（尺寸如图4），求图中阴影部分的面积，请给出解答过程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明家的洗手盆上装有一种抬启式水龙头（如图1），完全开启后，把手AM的仰角α=37°，此时把手端点A、出水口B和点落水点C在同一直线上，洗手盆及水龙头的相关数据如图2.（参考数据：sin37°=
，cos37°=
，tan37°=
）求把手端点A到BD的距离；
求CH的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，A(-1，5)，B(-2，0)，C(-4，3).
(1)请画出△ABC关于y轴对称的△A，B，C，，并写出点C的坐标；
(2)求△ABC的面积；
(3)在y轴上画出点P的位置，使线段PA+PB的值最小，并直接写出PA+PB的最小值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某种型号汽车油箱容量为40升，每行驶100千米耗油10升.设一辆加满油的该型号汽车行驶路程为x(千米)，行驶过程中油箱内剩余油量为y(升).
(1)求y与x之间的函数表达式；
(2)该辆汽车以80千米/时的速度从甲地出发开往距离甲地1050千米的B地，为了有效延长汽车使用寿命，厂家建议每次加油时，油箱内剩余油量不低于油箱容量的
，按此建议，求该辆汽车最多行驶多长时间就需再一次加油?此次加油后，剩余路程至少还需再加几次油?
相关试题
