【题目】某经营世界著名品牌的总公司,在我市有甲、乙两家分公司,这两家公司都销售香水和护肤品,总公司现有香水70瓶,护肤品30瓶,分配给甲、乙两家公司,其中40瓶给甲公司,60瓶给乙公司,且都能卖完,两公司的利润(元)如下表.
每瓶香水利润 | 每瓶护肤品利润 | |
甲公司 | 180 | 200 |
乙公司 | 160 | 150 |
(1)假设总公司分配给甲公司x瓶香水,求:甲、乙两家公司的总利W与x之间的函数解析式.
(2)在(1)的条件下,甲公司的利润会不会比乙公司的利润高?并说明理由.
(3)若总公司要求总利润不低于17370元,请问有多少种不同的分配方案,并将各种方案设计出来.
参考答案:
【答案】(1)W=-30x+17700(2)甲公司的利润不会比乙公司的利润高.(3)①当x=10时,总公司分配给甲公司香水10瓶,护肤品30瓶,乙公司香水60瓶,护肤品0瓶,②当x=11时,总公司分配给甲公司香水11瓶,护肤品29瓶,乙公司香水59瓶,护肤品1瓶.
【解析】【试题分析】
(1)设总公司分配给甲公司x瓶香水,护肤品(40-x)瓶,乙公司的香水和护肤品瓶数分别为(70-x)瓶,(x-10)瓶,根据表格里面的对应利润,得:W=180x+200(40-x)+160(70-x)+150(x-10)=-30x+17700即可;
(2)先表示出甲、乙两个公司利润,用作差法比较大小即可;
(3)根据(1)中,得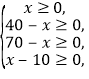 解得自变量的取值范围为:10≤x≤40.根据题意列出不等式得:由W=-30x+17700≥17370,得x≤11,从而确定x的取值范围10≤x≤11,故两种分配方案.
解得自变量的取值范围为:10≤x≤40.根据题意列出不等式得:由W=-30x+17700≥17370,得x≤11,从而确定x的取值范围10≤x≤11,故两种分配方案.
【试题解析】
(1)设总公司分配给甲公司x瓶香水,护肤品(40-x)瓶,乙公司的香水和护肤品瓶数分别为(70-x)瓶,(x-10)瓶,
W=180x+200(40-x)+160(70-x)+150(x-10)=-30x+17700.
故甲、乙两家公司的总利润W与x之间的解析式为W=-30x+17700.
(2)甲公司的利润为180x+200(40-x)=8000-20x,
乙公司的利润为160(70-x)+150(x-10)=9700-10x,
8000-20x-(9700-10x)=-1700-10x<0,
∴甲公司的利润不会比乙公司的利润高.
(3)由(1)得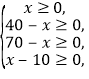 解得10≤x≤40.
解得10≤x≤40.
由W=-30x+17700≥17370,得x≤11,
∴10≤x≤11,
∴有两种不同的分配方案.
①当x=10时,总公司分配给甲公司香水10瓶,护肤品30瓶,乙公司香水60瓶,护肤品0瓶,
②当x=11时,总公司分配给甲公司香水11瓶,护肤品29瓶,乙公司香水59瓶,护肤品1瓶.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚家装修,准备安装照明灯.他和爸爸到市场进行调查,了解到某种优质品牌的一盏40瓦白炽灯的售价为1.5元,一盏8瓦节能灯的售价为22.38元,这两种功率的灯发光效果相当.假定电价为0.45元/度,设照明时间为x(小时),使用一盏白炽灯和一盏节能灯的费用分别为y1(元)和y2(元)[耗电量(度)=功率(千瓦)×用电时间(小时),费用=电费+灯的售价].
(1)分别求出y1,y2与照明时间x之间的函数表达式;
(2)你认为选择哪种照明灯合算?
(3)若一盏白炽灯的使用寿命为2000小时,一盏节能灯的使用寿命为6000小时,如果不考虑其他因素,以6000小时计算,使用哪种照明灯省钱?省多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】深圳今年4月份某星期的最高气温如下(单位℃):26,25,27,28,27,25,25,则这个星期的最高气温的众数和中位数分别是( )
A.25,26
B.25,26.5
C.27,26
D.25,28 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=
 S△ABF,其中正确的结论有________个。
S△ABF,其中正确的结论有________个。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某海滩景区门票价格为80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
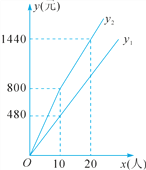
根据图象,回答下列问题:
(1)a= ,b=__ __.
(2)直接写出y1,y2与x之间的函数表达式.
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到该海滩景区旅游,两团共计50人,两次共付门票费用3040元,求A,B两个旅游团各有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评,A、B、C、D、E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评
 结果如表所示:
结果如表所示:表1演讲答辩得分表
 单位:分
单位:分
A
B
C
D
E
甲
90
92
94
95
88
乙
89
86
87
94
91
表2民主测评票数统计表
 单位:张
单位:张
“好”票数
“较好”票数
“一般”票数
甲
40
7
3
乙
42
4
4
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分
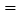 “好”票数
“好”票数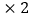 分
分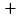 “较好”票数
“较好”票数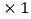 分
分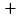 “一般”票数
“一般”票数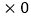 分;综合得分
分;综合得分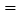 演讲答辩得分
演讲答辩得分 民主测评得分
民主测评得分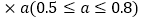 ;
;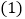 当
当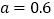 时,甲的综合得分是多少?
时,甲的综合得分是多少? 如果以综合得分来确定班长,试问:甲、乙两位同学哪一位当选为班长?并说明理由.
如果以综合得分来确定班长,试问:甲、乙两位同学哪一位当选为班长?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于
 AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF.
AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF.(1)求证:四边形AEDF是菱形;
(2)若BD=6,AF=4,CD=3,求BE的长。

相关试题

