【题目】如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为 . 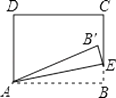
参考答案:
【答案】![]() 或15
或15
【解析】解:如图1,∵将△ABE沿AE折叠,得到△AB′E, 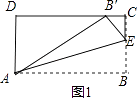
∴AB′=AB=5,B′E=BE,∴CE=3﹣BE,∵AD=3,∴DB′=4,∴B′C=1,∵B′E2=CE2+B′C2 ,
∴BE2=(3﹣BE)2+12 ,
∴BE= ![]() ,
,
如图2,∵将△ABE沿AE折叠,得到△AB′E,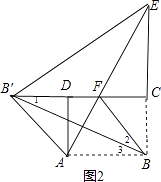
∴AB′=AB=5,
∵CD∥AB,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∵AE垂直平分BB′,
∴AB=BF=5,
∴CF=4,
∵CF∥AB,
∴△CEF∽△ABE,
∴ ![]() ,
,
即 ![]() =
= ![]() ,
,
∴CE=12,∴BE=15,
综上所述:BE的长为: ![]() 或15,
或15,
故答案为: ![]() 或15.
或15.
如图1,根据折叠的性质得到AB′=AB=5,B′E=BE,根据勾股定理得到BE2=(3﹣BE)2+12 ,
于是得到BE= ![]() ,如图2,根据折叠的性质得到AB′=AB=5,求得AB=BF=5,根据勾股定理得到CF=4根据相似三角形的性质列方程得到CE=12,即可得到结论.
,如图2,根据折叠的性质得到AB′=AB=5,求得AB=BF=5,根据勾股定理得到CF=4根据相似三角形的性质列方程得到CE=12,即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程ax2﹣(a+2)x+2=0有两个不相等的正整数根时,整数a的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知第一象限内的点A在反比例函数y=
 上,第二象限的点B在反比例函数y=
上,第二象限的点B在反比例函数y=  上,且OA⊥OB,tanA=
上,且OA⊥OB,tanA=  ,则k的值为 .
,则k的值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在
 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 .
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;

①把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
②以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5. 月信息消费额分组统计表
组别
消费额(元)
A
10≤x<100
B
100≤x<200
C
20≤x<300
D
300≤x<400
E
x≥400
请结合图表中相关数据解答下列问题:

(1)这次接受调查的有户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.

(1)求证:△CDP≌△POB;
(2)填空: ①若AB=4,则四边形AOPD的最大面积为;
②连接OD,当∠PBA的度数为时,四边形BPDO是菱形.
相关试题

