【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
参考答案:
【答案】(1)A种产品8件,B种产品2件;(2)6种方案(3)当![]() 时可获得最大利润,最大利润为26万元.
时可获得最大利润,最大利润为26万元.
【解析】
试题分析:(1)设生产A种产品x件,则生产B种产品有(10﹣x)件,根据计划获利14万元,即两种产品共获利14万元,即可列方程求解;
(2)根据计划投入资金不多于44万元,且获利多于14万元,这两个不等关系即可列出不等式组,求得x的范围,再根据x是非负整数,确定x的值,x的值的个数就是方案的个数;
(3)得出利润y与A产品数量x的函数关系式,根据增减性可得,B产品生产越多,获利越大,因而B取最大值时,获利最大,据此即可求解.
解:(1)设生产A种产品x件,则生产B种产品(10﹣x)件,于是有
x+3(10﹣x)=14,
解得:x=8,
则10﹣x=10﹣8=2(件)
所以应生产A种产品8件,B种产品2件;
(2)设应生产A种产品x件,则生产B种产品有(10﹣x)件,由题意有:
![]() ,
,
解得:2≤x<8;
所以可以采用的方案有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共6种方案;
,共6种方案;
(3)设总利润为y万元,生产A种产品x件,则生产B种产品(10﹣x)件,
则利润y=x+3(10﹣x)=﹣2x+30,
则y随x的增大而减小,即可得,A产品生产越少,获利越大,
所以当![]() 时可获得最大利润,其最大利润为2×1+8×3=26万元.
时可获得最大利润,其最大利润为2×1+8×3=26万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为执行“均衡教育”政策,某县2014年投入教育经费2500万元,预计到2016年底三年累计投入1.2亿元.若每年投入教育经费的年平均增长 百分率为x,则下列方程正确的是( )
A.2500(1+x)2=1.2 B.2500(1+x)2=12000
C.2500+2500(1+x)+2500(1+x)2=1.2 D.2500+2500(1+x)+2500(1+x)2=12000
-
科目: 来源: 题型:
查看答案和解析>>【题目】从十边形的一个顶点出发,可以引m条对角线,这些对角线可以把这个十边形分成n个三角形,则m+n=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形的周长为16cm,它两邻边长分别为xcm,ycm,且满足(x﹣y)2﹣2x+2y+1=0,求其面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7.
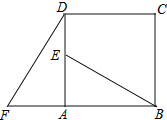
(1)求BE的长;
(2)在图中作出延长BE与DF的交点G,并说明BG⊥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,不能判断四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D B.AB∥CD,AB=CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一只不透明的盒子里有背面完全相同,正面上分别写有数字1、2、3、4的四张卡片,小马从中随机地抽取一张,把卡片上的数字作为被减数;在另一只不透明的盒子里将形状、大小完全相同,分别标有数字1、2、3的三个小球混合后,小虎从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小马与小虎做游戏,规则是:若这两数的差为非正数,则小马赢;否则小虎赢.你认为该游戏公平吗?请说明理由.
相关试题

