【题目】如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,连结
的中点,连结![]() ,点
,点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 运动,到点
运动,到点![]() 停止,点
停止,点![]() 在
在![]() 上以
上以![]() 的速度运动,在
的速度运动,在![]() 上以
上以![]() 的速度运动,过点
的速度运动,过点![]() 作
作![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() .
.
(![]() )当点
)当点![]() 在线段
在线段![]() 上运动时,线段
上运动时,线段![]() 的长为__________
的长为__________![]() .(用含
.(用含![]() 的代数式表示)
的代数式表示)
(![]() )当正方形
)当正方形![]() 与
与![]() 重叠部分图形为五边形时,设五边形的面积为
重叠部分图形为五边形时,设五边形的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.
(![]() )如图
)如图![]() ,若点
,若点![]() 在线段
在线段![]() 上,且
上,且![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径作圆,当点
长为半径作圆,当点![]() 开始运动时,⊙
开始运动时,⊙![]() 的半径以
的半径以![]() 的速度开始不断增大,当⊙
的速度开始不断增大,当⊙![]() 与正方形
与正方形![]() 的边所在直线相切时,求此时的
的边所在直线相切时,求此时的![]() 值.
值.
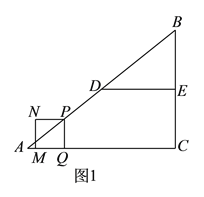
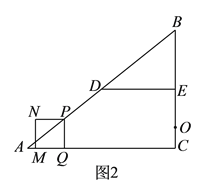
参考答案:
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ;(
;(![]() )
)![]()
【解析】试题分析:(1)点P在AD段的运动时间为1s,则DP的长度为(t-1)cm;(2)当正方形PQMN与△ABC重叠部分图形为五边形时,有一种情况,分别用时间t表示各相关运动线段的长度,如图利用“![]() 求出面积S的表达式;(3) 分两种情况讨论:①当圆与边
求出面积S的表达式;(3) 分两种情况讨论:①当圆与边![]() 相切时和②当圆与
相切时和②当圆与![]() 相切时,求相应t的值.
相切时,求相应t的值.
试题解析:(![]() )在
)在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 中点,
中点,
∴![]() ,
,
∴点![]() 在
在![]() 段的运动时间为
段的运动时间为![]() ,
,
当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 段的运动时间为
段的运动时间为![]() ,
,
∵![]() 段运动速度为
段运动速度为![]() ,∴
,∴![]() ,
,
∴答案为![]() .
.
(![]() )当正方形
)当正方形![]() 与
与![]() 重叠部分图形为五边形时,有一种情况,如下图所示.
重叠部分图形为五边形时,有一种情况,如下图所示.
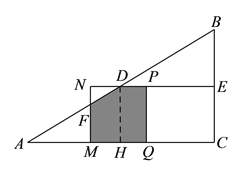
当正方形的边长大于![]() 时,重叠部分为五边形,
时,重叠部分为五边形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]() .
.
(![]() )①当圆与边
)①当圆与边![]() 相切时,如下图,
相切时,如下图,
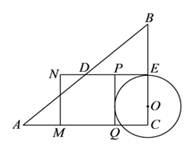
当圆与![]() 相切时,
相切时,![]() ,
,
由(![]() )可知,
)可知,![]() ,
,
∴![]() ,
,
∵![]() 以
以![]() 的速度不断增大,
的速度不断增大,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() .
.
②当圆与![]() 相切时,
相切时,
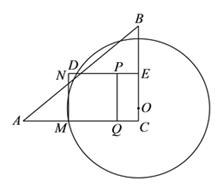
此时,![]() ,由(
,由(![]() )可知,
)可知,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() 到
到![]() 点停止,
点停止,
∴![]() ,
,![]() ,
,
∴![]() (舍),
(舍),
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点(n,3)在一次函数y=2x﹣1的图象上,则n的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点A(1,2).
(1)求m、n的值;
(2)设l1交x轴于点B,l2交x轴于点C,若点D与点A,B,C能构成平行四边形,请直接写出D点坐标;
(3)请在所给坐标系中画出直线l1和l2 , 并根据图象回答问题:
当x满足时,y1>2;
当x满足时,0<y2≤3;
当x满足时,y1<y2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】点A在x轴的下方,y轴的右侧,到x轴的距离是3,到y轴的距离是2,则点A的坐标是( )
A.(2,﹣3)
B.(2,3)
C.(3,﹣2)
D.(﹣3,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数的平方根是2a﹣7和a+4,求这个正数 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某细胞的直径为0.00000015米,这个数用科学记数法表示为___________米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°.
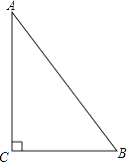
(1)在BC边上作一点P,使得点P到点C的距离与点P到边AB的距离相等(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=8,BC=6,求CP的长.
相关试题

