Question

【题目】如图：直线y=-x+5分别与轴、轴交于A、B两点．

（1）求A、B两点的坐标；

（2）已知点C坐标为（4,0），设点C关于直线AB的对称点为D，请直接写出点D的坐标；

（3）请在直线AB找一点M和轴上找一点N，使△CMN的周长最短，求出点N的坐标和△CMN的周长．

Answer 1

【答案】（1）A（5，0）；B（0，5）；（2）D（5，1）；（3）N(0，) ；

【解析】

（1）令x=0，则y=5；令y=0，则x=5，即可求得；（2）首先根据直线AB的解析式可知△OAB是等腰直角三角形，然后根据轴对称的性质即可求出点D的坐标；（3）作出点C关于直线y轴的对称点C′，连接DE交AB于点M，交y轴于点N，则此时△CMN的周长最短．由D、E两点的坐标利用待定系数法求出直线DC′的解析式，再根据y轴上点的坐标特征，即可求出点N的坐标．

(1) ∵直线分别与轴、轴交于A、B两点

令，则；令，则

∴点A坐标为（5,0）、点B 坐标为（0, 5）；

(2)如图：过A作直线l⊥x轴，作CD⊥AB交直线l于D，

∵OA=OB=5，

∴∠OAB=45°，

∵CD⊥AB，直线l⊥x轴，

∴∠DCA=45°，∠DAB=45°

∴∠CDA=45°，

∴AD=AC，

∵AB⊥CD，

∴AB垂直平分CD，

∴D即是C关于AB的对称点，

∵A（5，0），C（4，0）

∴AC=AD=1，

∴ 点C 关于直线AB的对称点D的坐标为（5，1），

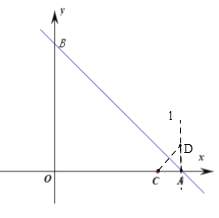
(3) 作点C关于轴的对称点C′，则C′的坐标为（-4,0）

连接C′D交AB于点M，交轴于点N，

∵点C、C′关于轴对称

∴NC= NC′，

∵点C、D关于直线AB对称，

∴CM=DM，

此时，△CMN的周长=CM+MN+NC= DM +MN+ NC′= DC′周长最短；

设直线C′D的解析式为

∵点C′的坐标为（-4,0），点D的坐标为（5,1）

∴，解得

∴直线C′D的解析式为，

与轴的交点N的坐标为 (0，)

根据勾股定理，或两点间距离公式可求 △CMN的周长