搜索
【题目】若5k+20＜0，则关于x的一元二次方程x2+4x﹣k=0的根的情况是（ ）
A. 没有实数根 B. 有两个相等的实数根
C. 有两个不相等的实数根 D. 无法判断
参考答案：
【答案】A
【解析】
根据已知不等式求出k的范围，进而判断出根的判别式的值的正负，即可得到方程解的情况．
解：∵5k+20＜0，即k＜-4，
∴△=16+4k＜0，
则方程没有实数根．
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知∠α＝35°，那么∠α的余角等于( )
A、35° B、55° C、65° D、145°
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于抛物线y=(x-1)2-2，下列说法中错误的是（ ）
A.顶点坐标为(1，-2)
B.对称轴是直线x=1
C.当x＞1时，y随x的增大而减小
D.开口方向向上 -
科目： 来源： 题型：
查看答案和解析>>【题目】多项式2a3+b2﹣ab3的次数是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了打造区域中心城市，实现跨越式发展，我市新区建设正按投资计划有序推进．新区建设工程部，因道路建设需要开挖土石方，计划每小时挖掘土石方540m3，现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，租赁公司提供的挖掘机有关信息如表：
（1）若租用甲、乙两种型号的挖掘机共8台，恰好完成每小时的挖掘量，则甲、乙两种型号的挖掘机各需多少台？
（2）如果每小时支付的租金不超过850元，又恰好完成每小时的挖掘量，那么共有几种不同的租用方案？
-
科目： 来源： 题型：
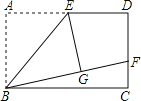
查看答案和解析>>【题目】如图，矩形ABCD中，E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F．若AB=6，BC=10，则FD的长为（ ）
A．
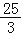B．4 C．
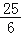D．5 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A（a，1）、B（﹣1，b）都在函数
（x＜0）的图象上，点P、Q分别是x轴、y轴上的动点，当四边形PABQ的周长取最小值时，PQ所在直线的解析式是 ．
相关试题
