Question

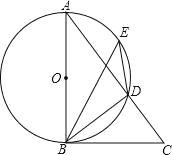
【题目】如图，AB是⊙O的直径，点E是上的一点，∠DBC=∠BED．

（1）求证：BC是⊙O的切线；

（2）已知AD=3，CD=2，求BC的长．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

试题分析：（1）AB是⊙O的直径，得∠ADB=90°，从而得出∠BAD=∠DBC，即∠ABC=90°，即可证明BC是⊙O的切线；

（2）可证明△ABC∽△BDC，则，即可得出BC=．

试题解析：（1）∵AB是⊙O的切直径，

∴∠ADB=90°，

又∵∠BAD=∠BED，∠BED=∠DBC，

∴∠BAD=∠DBC，

∴∠BAD+∠ABD=∠DBC+∠ABD=90°，

∴∠ABC=90°，

∴BC是⊙O的切线；

（2）解：∵∠BAD=∠DBC，∠C=∠C，

∴△ABC∽△BDC，

∴，即BC2=ACCD=（AD+CD）CD=10，

∴BC=．