【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N,设∠AEM=α(0°<α<90°),给出下列四个结论:
①AM=CN;②∠AME=∠BNE;③BN﹣AM=2;④S△EMN=![]() .
.
上述结论中正确的个数是( )
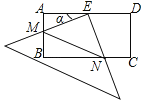
A.1 B.2 C.3 D.4
参考答案:
【答案】C.
【解析】
试题分析:①如图,在矩形ABCD中,AD=2AB,E是AD的中点,作EF⊥BC于点F,则有AB=AE=EF=FC,∵∠AEM+∠DEN=90°,∠FEN+∠DEN=90°,∴∠AEM=∠FEN,在Rt△AME和Rt△FNE中,∵∠AEM=∠FEN,AE=EF,∠MAE=∠NFE,∴Rt△AME≌Rt△FNE,∴AM=FN,∴MB=CN.
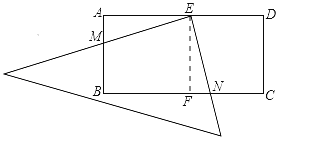
∵AM不一定等于CN,∴AM不一定等于CN,∴①错误,②由①有Rt△AME≌Rt△FNE,∴∠AME=∠BNE,∴②正确,③由①得,BM=CN,∵AD=2AB=4,∴BC=4,AB=2
∴BN﹣AM=BC﹣CN﹣AM=BC﹣BM﹣AM=BC﹣(BM+AM)=BC﹣AB=4﹣2=2,∴③正确,④如图,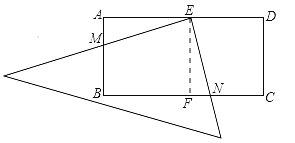
由①得,CN=CF﹣FN=2﹣AM,AE=![]() AD=2,AM=FN
AD=2,AM=FN
∵tanα=![]() ,∴AM=AEtanα
,∴AM=AEtanα
∵cosα=![]() =
=![]() ,∴
,∴ ![]() ,∴
,∴![]() =1+
=1+![]() =1+
=1+![]() =1+
=1+![]() ,∴
,∴![]() =2(1+
=2(1+![]() )
)
∴S△EMN=S四边形ABNE﹣S△AME﹣S△MBN
=![]() (AE+BN)×AB﹣
(AE+BN)×AB﹣![]() AE×AM﹣
AE×AM﹣![]() BN×BM
BN×BM
=![]() (AE+BC﹣CN)×2﹣
(AE+BC﹣CN)×2﹣![]() AE×AM﹣
AE×AM﹣![]() (BC﹣CN)×CN
(BC﹣CN)×CN
=![]() (AE+BC﹣CF+FN)×2﹣
(AE+BC﹣CF+FN)×2﹣![]() AE×AM﹣
AE×AM﹣![]() (BC﹣2+AM)(2﹣AM)
(BC﹣2+AM)(2﹣AM)
=AE+BC﹣CF+AM﹣![]() AE×AM﹣
AE×AM﹣![]() (2+AM)(2﹣AM)
(2+AM)(2﹣AM)
=AE+AM﹣![]() AE×AM+
AE×AM+![]()
![]()
=AE+AEtanα﹣![]()
![]() tanα+
tanα+![]()
![]()
![]()
=2+2tanα﹣2tanα+2![]()
=2(1+![]() )
)
=![]() ,∴④正确.
,∴④正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△AFD和△CEB中,点A、E、F、C在同一条直线上.有下面四个论断:
(1)AD=CB,(2)AE=CF,(3)∠B=∠D,(4)AD∥BC.
请用其中三个作为条件,余下一个作为结论,进行证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣23表示的意义是( ).
A. (﹣2)×(﹣2)×(﹣2) B. (﹣2)+(﹣2)+(﹣2)
C. (﹣2)×3 D. ﹣2×2×2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
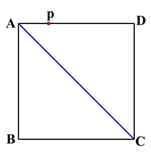
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP=
 ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市水稻的亩产量,随机抽取六块试验田进行调查,它们的亩产量分别为(单位:斤):1000,1100,
1250,1050,1100,1200,则这组数据的众数为斤. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四人进行100m短跑训练,统计近期10次测试的平均成绩都是13.2s,10次测试成绩的方差如下表则这四人中发挥最稳定的是( )
选手
甲
乙
丙
丁
方差(s2)
0.020
0.019
0.021
0.022
A.甲B.乙C.丙D.丁
相关试题

